問 題
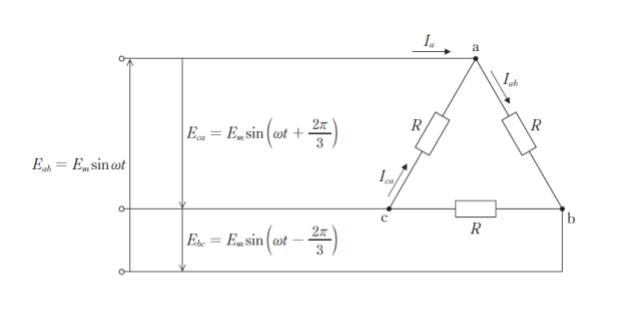


正解 (4)
解 説
㋐ ですが
問題文における Iab は、オームの法則 V = RI より、I = V/R なので、図における Eab = Em sin ωt を 公式の V に代入して求めていると考えられます。 同様に考えれば、Ica = Eca/R = (Em/R) × sin(ωt + 2π/3) です。正解は 3 ~ 5 です。
㋑ ですが
問題文にあるように Ia = Iab – Ica なので、Ia = (Em/R) × sin(ωt) – (Em/R) × sin(ωt + 2π/3) =(Em/R)(sin ωt – sin(ωt + 2π/3)) です。
太字部分の ( ) の中身について考えます。具体的に考えるのがおすすめです。ωt = 0 の時を考えます。sin ωt – sin(ωt + 2π/3) → sin0 – sin (2π/3) = -√3/2 です。
選択肢 3 ~ 5 に
ωt = 0 を代入すると、sin0 = 0、sin (-π/6) = -1/2 です。従って、Em/R の係数が -√3/2 となるのは、選択肢 4 です。
以上より、正解は 4 です。

コメント