2019年国家一般職(電気・電子・情報) No.23解説

　問題　　　　　

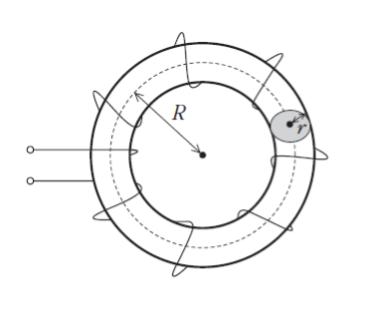
図のように、磁性体に導線が一様に巻かれた環状コイルがある。コイルの平均半径を R、磁性体の断面の半径を r、コイルの巻数を一定とするとき、このコイルの自己インダクタンス L に関する記述として最も妥当なのはどれか。ただし、R は r より十分大きいものとし、磁束は磁性体の外部に漏れないものとする。

正解 (2)

　解説　　　　　

環状ソレノイドが出てきたら、内部の磁界の強さ H = NI/2πr ・・・(1) をまずは思い出します。本問では小文字でなく大文字の R が (1) の r と対応します。

次にインダクタンスについて「電流流れて磁界発生 → 回路をどれだけ磁束が貫くかを考える」が基本です。

「磁束」に至るまでの流れは
・磁束密度 B について
材料の透磁率 μ として B = μH

→ 貫く断面積を S とする。本問の環状ソレノイドでは S = πr²
磁束 Φ (ファイ) = B × S ・・・(2) となります。

「コイル全体をどれだけ磁束が貫くか」を表す「磁束鎖交数 Ψ (プサイ)」について、環状ソレノイドでは NΦ です。Ψ = LＩとした時の L が自己インダクタンスとなります。

以上をふまえると、環状ソレノイドの自己インダクタンスは、式 (1) の所で R が分母に出てきて、R と自己インダクタンスは反比例の関係となります。つまり、R が ◯ 倍になると、自己インダクタンスは 1/◯ 倍です。

また、式 (2) の所で r が関係して、r の 2 乗と自己インダクタンスが比例します。つまり、r が △倍になると、自己インダクタンスは △² 倍になります。

従って
選択肢の中で妥当な記述は「R を 2 倍にしたとき、L は1/2 倍になる」です。

以上より、正解は 2 です。

コメント