問 題
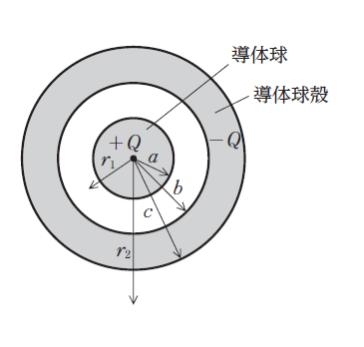
図のように、真空中に半径 a の導体球と内半径 b、外半径 c の導体球殻が同心状に置かれている。導体球に +Q (Q > 0) の電荷、導体球殻に -Q の電荷が与えられているとき、導体球及び導体球殻の中心からの距離 r1 (a < r1 < b) における電界の大きさ E1 及び距離 r2 (c < r2) における電界の大きさ E2 の組合せとして最も妥当なのはどれか。ただし、真空の誘電率を ε0 とする。
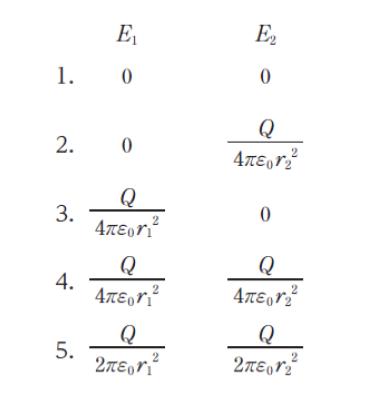
正解 (3)
解 説
電界 E はガウスの法則で求めます。
・半径 r1 の球による閉曲面を考えます。内側の電荷の総和が +Q です。ガウスの法則より、まず左辺が 球の表面積 4πr12 × E です。右辺は電荷の総和 ÷ ε0 です。つまり「4πr12E = Q/ε0」が成立します。従って、E1 = Q/4πε0r12 です。
・半径 r2 の球による閉曲面を考えます。内側の電荷の総和が +Q + -Q = 0 です。ガウスの法則より 4πr22E = 0/ε0 が成立します。従って、E2 = 0 です。
以上より、正解は 3 です。
類題 H29 no21 誘電体球の電荷
https://yaku-tik.com/koumuin/h29-denjyou-21/

コメント