R5年 汚水処理特論 問1 問題と解説

　問 題　　　　　

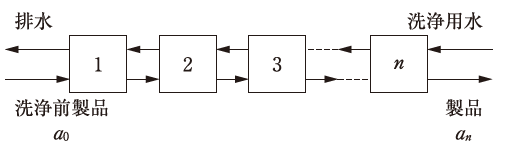
図に示すようなn段の向流多段洗浄においては、下に示す理論式が成り立つ。

ただし、

• a₀：洗浄前製品中に含まれる不純物質量
• a_n：第n段の洗浄槽を出る製品中の不純物質量
• r：洗浄水量Vと製品が各段で持ち出す水量vの比(r＝V/v)

今、rが50である洗浄工程において、製品中に含まれる不純物質量を洗浄前の1/10000以下に減らしたいとき、向流多段洗浄の段数を最低いくつにすればよいか。以下の選択肢から適切なものを選びなさい。

1. 2段
2. 3段
3. 4段
4. 5段
5. 10段

 

 

 

 

 

　解 説　　　　

本問では理論式が与えられているので、これを利用して計算を進めていけば答えを出すことができます。

まず、問題文より「r＝50」なので、与えられている理論式に代入すると、次に示す(1)式となります。

次に、製品中に含まれる不純物質量を洗浄前の1/10000以下に減らすということなので、次に示す(2)式が成り立ちます。

そして、(1)を(2)に代入して式を整理していくと、以下のように表すことができます。

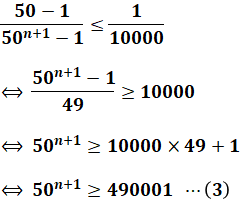
ここで、50²＝2500、50³＝125000、50⁴＝6250000なので、(3)式が成り立つのは「n＋1」が4以上のときです。つまり、nは最低3であることがわかります。

以上から、正解は(2)の「3段」となります。