問 題
多数の円柱状捕集体を持つ障害物形式の集じん装置の集じん率ηを表す式として、正しいものはどれか。
ただし、A:ダスト捕集体の全表面積、V:捕集体が充塡(じゅうてん)されている装置の体積、L:装置長さ、α:捕集体充塡率、ηt:単一捕集体捕集効率とする。
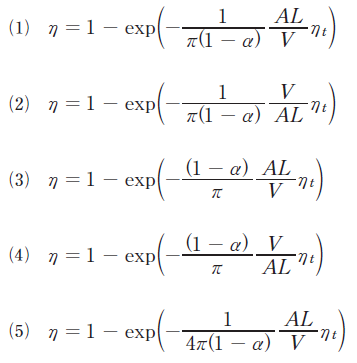
解 説
前の問題(問5)に出てきたドイッチェの式などは重要公式として押さえておきたいですが、この問題では「多数の円柱状捕集体を持つ障害物形式の集じん装置の集じん率ηを表す式」という、かなりマイナーな式が出題されています。
そのため、この問題は捨て問題扱いにしてしまっても構わないと個人的には思います。ただし、変数の増減に伴う集じん率の増減を考えることで、選択肢(1)、(5)の2択までは絞りたいです。
というのも、式の形はどれも「η=1-eのマイナス何乗」となっているので、「何乗」の部分が大きいほど「eのマイナス何乗」の部分が小さくなり、集じん率ηは大きくなります。
一方、各パラメータのA、V、L、αが増加すると集じん率ηがどうなるかを考えると次のようになります。
- A:ダスト捕集体の全表面積が大きいとダストを引っ掛けやすくなるので、ηは大きくなる
- V:装置の体積が大きくなると捕集体の密度がすかすかになるので、ηは小さくなる
- L:装置の長さが長くなれば、それだけダストを捕集するチャンスが増えるので、ηは大きくなる
- α:捕集体充塡率が高いと、それだけ捕集体が充実しているので、ηは大きくなる
以上を踏まえると、AとLは「何乗」の部分、つまりexpの( )内において、分子にくることがわかります。また、反対にVは分母にきます。
この段階で、選択肢(1)、(3)、(5)の3択に絞ることができました。
そしてαについては、αが大きいと(1-α)が小さくなります。この場合の結論としては集じん率ηが大きくなるはずなので、「何乗」の部分も大きくしたいです。そのためには、αが大きいほど小さくなっていく(1-α)を、分母に置けばよいことがわかります。
よって、(1)、(3)、(5)のうち、(3)は不適です。
このように考えることで、選択肢(1)、(5)の2択に絞ることができました。本番の試験でこのようなマイナーな問題が出たら、ここまでやれば十分だと思います。
一応正解を示しておくと、(1)が正しい式なので、これが正解となります。

コメント