問 題
障害物形式集じん装置の集じん率ηを表現する式として、正しいものはどれか。
ただし、c:装置で決まる定数、A:ダストが捕集される障害物の全表面積、V:障害物が充塡されている装置の体積、L:装置長さ、ηt:障害物1個当たりの捕集効率、である。
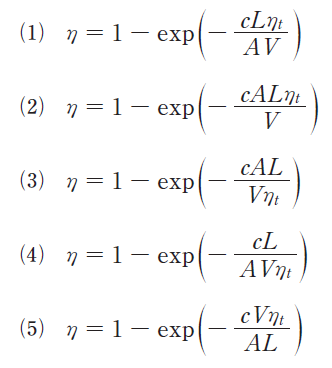
正解 (2)
解 説
R4 問4などで出題されたドイッチェの式(電気集じん装置の集じん率ηの推定式)は重要公式として押さえておきたいですが、この問題では「電気集じん装置」ではなく「障害物形式集じん装置」の式が出題されています。
これはドイッチェの式と比べてマイナーなため馴染みはないと思いますが、各変数の増減に伴う集じん率ηの増減を考えることで正解を選ぶことができる問題です。
というのも、式の形はどれも「η=1-eのマイナス何乗」となっているので、「何乗」の部分が大きいほど「eのマイナス何乗」の部分が小さくなり、集じん率ηは大きくなります。
一方、各パラメータのA、V、L、ηtが増加すると集じん率ηがどうなるかを考えると次のようになります。
- A:ダスト捕集体の全表面積が大きいとダストを引っ掛けやすくなるので、ηは大きくなる
- V:装置の体積が大きくなると捕集体の密度がすかすかになるので、ηは小さくなる
- L:装置の長さが長くなれば、それだけダストを捕集するチャンスが増えるので、ηは大きくなる
- ηt:捕集効率が高いとそれだけ捕集しやすくなるので、ηは大きくなる
以上を踏まえると、AとLとηtは「何乗」の部分、つまりexpの( )内において、分子にくることがわかります。また、反対にVは分母にきます。
よって、それを満たす選択肢(2)が正解であると判断することができます。
以上から、正解は(2)です。

コメント