三角比を含む計算問題の中には、sinθやcosθの「θ」の部分が複雑なものになっているときがあります。具体的には、sin(-θ)やcos(π/2-θ)、sin(π-θ)といったようなものが挙げられます(ほかにも色々あります)。
このような場合、( )の中をすっきりさせるための変換式があります。これらは、三角比の負角の公式、余角の公式、補角の公式などと呼ばれていますが、基本的な公式だけでも合計で十数個ある上、どれも似たような式で混乱しやすいので、これらを全部暗記に頼るのは現実的ではありません。
そこで、この項では、このように三角比の角度の部分が複雑なとき、単位円を使って簡単化する方法を紹介します。単位円を使って考えることができれば、上記で話題にした十数個の公式は全く覚えなくて大丈夫です。
負角の三角比
負角というのは、文字通りマイナスの角度という意味です。別に名前は重要じゃないので、気にしないで構いません。
sin(-θ)やcos(-θ)のような負角の三角比をそのままにしておくと計算しづらい場合、次のように変換することができます。
![]()
![]()
ただし、繰り返しになりますが、これを公式として覚えておく必要はありません。それは、以下の単位円を使えば、上式が成り立つのは一目瞭然だからです。
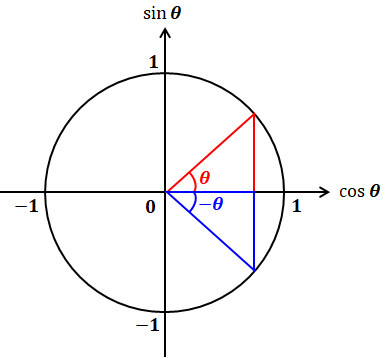
つまり、単位円における横軸がcosの値なので、角度が「θ」であっても「-θ」であっても横軸の値は変わりません。一方、縦軸がsinの値なので、「θ」と「-θ」とでは、sinの値の正負が全く反対になります。よって、最初に示したような式が成り立ちます。
余角の三角比
直角三角形の2つの鋭角のうち、一方を「θ」とすると、他方は「π/2-θ」になります。このとき「π/2-θ」のほうを「θ」に対する余角といいますが、ある角と余角との関係式を以下のように表すことができます。
![]()
![]()
これも公式として覚えるのではなく、単位円から考えることができます。
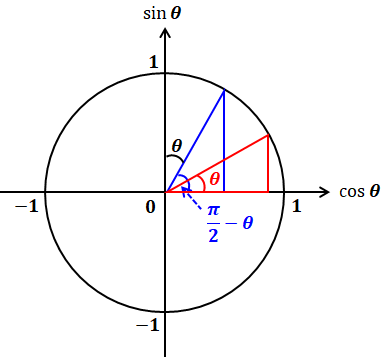
上図を見てわかるように、「π/2-θ」を使った青色の直角三角形と、「θ」を使った赤色の直角三角形は合同であり、回転させると2つの直角三角形がぴったり重なります。
また、2つの三角形は横軸の値と縦軸の値が全く反対(青色のsinが赤色のcos、青色のcosが赤色のsin)なので、
![]()
![]()
が成り立つことがわかります。
補角の三角比
2つの角度が合わせてπになるとき、一方が「θ」なら、他方は「π-θ」になります。このとき「π-θ」を補角といいますが、sinについては「θ」でも「π-θ」でも同じ値となります。一方、cosの場合は、「θ」と「π-θ」とで値が全く反対になります。
このことについて、以下の単位円を見ながら考えてみてください。
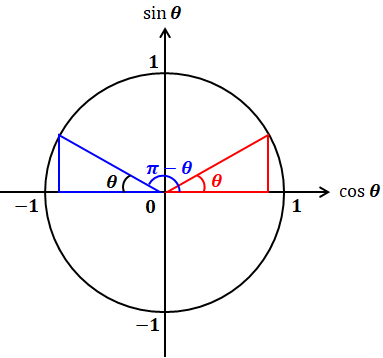
上図を見てわかる通り、「θ」と「π-θ」とでは、縦軸は変わらず、横軸は正負が反対になります。
よって、
![]()
![]()
という変換式が成り立つことがわかります。
負角、余角、補角を使った変換式には上記で紹介したもの以外にも様々なパターンが存在しますが、どれも上記と同じように単位円を描いて、どことどこが一緒、あるいは符号が変わる…などを考えていけば、どういう変換をすればよいのか考えることができるはずです。

コメント