電験三種の計算問題の過程では、分数の分母や分子自体が分数となっている、いわゆる二重分数がたびたび登場します。この項では、二重分数をどのように処理したらよいかについて解説します。
まず、結論から書くと、二重分数は次のように計算することができます。
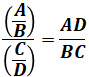
上式にある通り、「分子の中の分母」は最終的に分母側に回り、「分母の中の分母」は最終的に分子側に回ります。要するに、分子と分母それぞれの分母側が、反対側に移動する…ということもできます。
この式が成り立つことをすんなり理解できている場合は、この項で扱う内容は問題ありません。次へお進みください。もし上式がいまいちピンとこない場合には、引き続き以下の解説をお読みください。
分数の計算を一例挙げると、次のようなものがあります。
![]()
これなら誰でも解けると思いますが、この式の意味するところは、10÷2で、答えは5になります。
つまり、分数の計算とは「分子÷分母」で成り立つといえますが、これを割り算ではなく掛け算で考えることもできます。そのやり方は、「÷」を「×」に変えるのと同時に、その後ろの数の分母と分子を入れ替える…というものです。先ほどの例を用いると、次のように書くことができます。
![]()
同様のことを別の計算例で示すと、次のようなものが挙げられます。
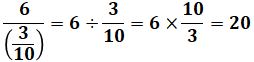
このように計算することによって、それぞれの数字が最終的にどこに納まるのかがわかりやすくなると思います。
以上のことから、この項の最初の例に戻ると、次のような計算過程によって二重分数を計算することができます。
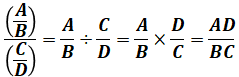

コメント