角度の表し方
この項では三角比について解説をしますが、その前に角度の2つの表し方を押さえておかなくてはなりません。
角度には、度(単位は[°])とラジアン(単位は[rad])とがあります。円を1周するための角度は周知の通り360[°]ですが、これをラジアンで考えると、1周で2π[rad]となります。
よって、角度とラジアンの関係は次のようになります。

三角比の基礎
直角三角形があるとき、1辺の長さと角度がわかっていれば、残る2辺の長さを知ることができます。また、直角三角形の3辺のうち2辺の長さがわかっていれば、残る1辺の長さと角度を知ることができます。
これらを導出するために使われる考え方が、以下に解説する三角比です。
三角比には、sin(サイン)、cos(コサイン)、tan(タンジェント)という3つの種類がありますが、それぞれの定義は、次の図と式で表している通りです。
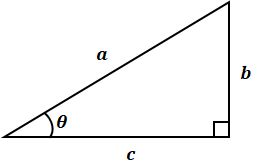
![]()
上記を押さえておけば、たとえばθとaがわかっているときは、sinの式からbが計算できます。さらに、cを知るためには、三平方の定理かcosの式かtanの式のいずれかを使って求めることができます。
同様に、たとえばaとcがわかっているときには、cosの式からθがわかります。そして、bを知るためには、三平方の定理かsinの式かtanの式のいずれかを使えば計算することができます。
θ=0、90°のときの三角比
また、極端な例として、θ=0のときやθ=90[°](π/2[rad])のときを考えてみてください。
まずはθ=0とするため、上図に示した直角三角形のθを段々小さくして、三角形が潰れていくところを想像してください。すると、θ=0となった時点で、斜辺のaと底辺のcがぴったりと重なり、bの部分がなくなります(a=c、b=0)。よって、このときのsinとcosの値は、
![]()
![]()
となります。
また、θ=90[°](π/2[rad])のときも同様に考えると、今度はaとbが重なって、cが消えます(a=b、c=0)。よって、このときのsinとcosの値は、
![]()
![]()
となります。

コメント