電験三種 R6年度上期 理論 問15 問題と解説

　問 題　　　　　

図の交流回路において、回路素子は、インダクタンスLのコイル又は静電容量Cのコンデンサである。この回路に正弦波交流電圧v＝500sin(1000t)[V]を加えたとき、回路に流れる電流は、i＝50cos(1000t)[A]であった。

このとき、次の(a)及び(b)の問に答えよ。

(a)　回路素子の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. C＝10nF
2. C＝100nF
3. C＝10μF
4. L＝10mH
5. L＝100mH

(b)　この回路素子に蓄えられるエネルギーの最大値W_maxの値[J]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、インダクタンスの場合には1/2 Li²の、静電容量の場合には1/2 Cv²のエネルギーが蓄えられるものとする。

1. 2.5
2. 6.25
3. 12.5
4. 25
5. 125

 

 

 

 

 

　解 説 (a)　　　

本問では、この回路素子がコイルかコンデンサかわかっていません。そのため、まずは相電圧・相電流の位相関係からコイルかコンデンサかを判定し、その後、その大きさを求めます。

問題文より、この回路に加わる電圧と電流は次の(1)式、(2)式の通りです。

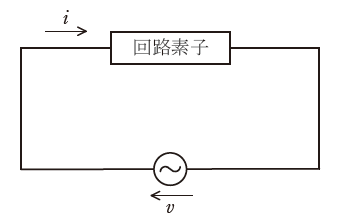
ここで、(2)式はcosの式になっていますが、(1)式と揃えるためにsinの式に変換します。また、見やすくするために各周波数をω(＝1000)[rad/s]とおくと、(2)式は次に示す(3)式のようになります。

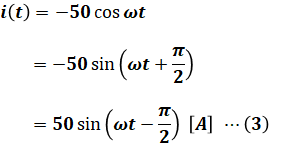
よって、(1)式の電圧と(3)式の電流を比べると、電流は電圧よりもπ/2(90°)だけ遅れている形となっていることがわかります。これは、回路素子がコイルを表しています(もしコンデンサなら電流が電圧よりも90°進むはずです)。

これで答えが(4)「L＝10mH」か(5)「L＝100mH」に絞られました。続いて、(4)と(5)のどちらが正しいかを考えていきます。

この回路には電源とコイルしかないので、コイルのリアクタンスX_L[Ω]は、次の(4)式によって求めることができます。

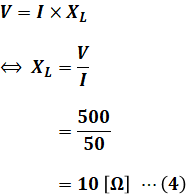
よって、コイルのインダクタンスL[H]は次の(5)式のように算出できます。これが問われている「回路素子の値」となります。

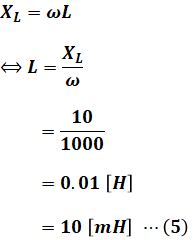
以上から、正解は(4)です。

　解 説 (b)　　　

設問(b)は設問(a)を間違えると正解できない一方、(a)が解ければとても簡単なサービス問題です。

(a)で回路素子がコイルだとわかっているので、問題文で与えられた式「W_max＝1/2 Li²[J]」を使えば、求めたいエネルギーW_max[J]を計算することができます。

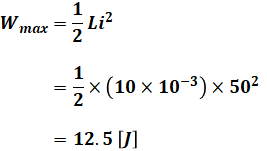
よって、正解は(3)となります。