問 題
円筒形三相同期電動機において、電動機の励磁電流を調整して、遅れ力率θで運転しているものとする。
このとき、供給電圧
、電機子電流
としたとき、誘導起電力
、並びに同期リアクタンスによる電圧降下
の関係を示すベクトル図として、正しいものを次の(1)～(5)のうちから一つ選べ。
なお、同期リアクタンスの大きさに対して巻線抵抗は十分小さいとみなせるものとする。
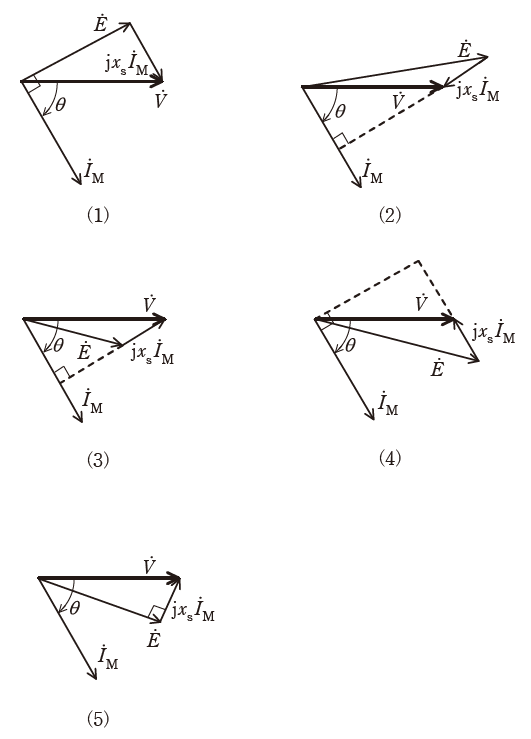
解 説
まず、同期電動機の1相あたりの等価回路を以下に示します。
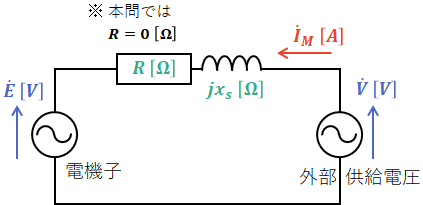
問題文より、この同期電動機は遅れ力率θで運転しているため、供給電圧のベクトルに対して時計回りにθだけ回転した向きが電機子電流の方向となります。実際、選択肢(1)～(5)がいずれもそのように描かれています。
また、上図の回路図にキルヒホッフの第二法則(電圧則)を用いると、以下の等式が成り立ちます。なお、本問では巻線抵抗が十分小さいので、以下ではR[Ω]を無視して考えます。
蛇足ですが、今回は電動機なので上記の(1)式が成り立ちますが、発電機の場合は電流の向きが反対になるので、等式は下式のように変化します。
本題に戻ると、(1)式より、はとの和となります。選択肢(1)～(5)の全てがこれを満たしているので、現時点ではまだ一つも除外できません。
ここで、本問では巻線抵抗R＝0[Ω]なので、電圧降下の向きは電機子電流の向きは垂直の関係になります。そのため、選択肢(2)か(3)が正しく、ほかは誤りであると判断できます。
なお、厳密にいえば電圧降下の向きは電機子電流より＋90°の進みとなるので、この時点で選択肢(2)が誤りで(3)が正しいとわかりますが、進みか遅れか迷っても次のように考えれば大丈夫です。
選択肢(2)と(3)の目立った違いは、(2)ではのほうがより大きく、(3)ではのほうがよりも大きいことです。
そして、外部から供給された電圧から、電圧降下によっていくらか減らされたものが誘導起電力だということを考えると、大きさを比べると＞となるはずです。よって、選択肢(2)と(3)では(3)のほうが適切であるとわかります。
以上から、正解は(3)となります。
コメント