電験三種 R5年度下期 機械 問2 問題と解説

　問 題　　　　　

界磁に永久磁石を用いた小形直流電動機がある。この電動機の電機子に12Vの電圧を加えたところ、無負荷の状態で3000min^－1で回転した。この電圧を維持したまま負荷を与えて、2Aの電機子電流を流したところ、損失が3W発生した。

この時の回転数[min^－1]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、ブラシの接触による電圧降下及び電機子反作用は無視できるものとし、損失は電機子巻線の銅損しか存在しないものとする。

1. 2250
2. 2625
3. 2813
4. 3000
5. 3429

 

 

 

 

 

　解 説　　　　

直流電動機の回転数は、負荷がかかると電機子電流が流れるために、銅損によって回転数が低下します。この設問では無負荷の状態で3000[min^－1]だった回転数が、負荷時にはいくらになるか…ということを聞いています。つまり、3000以上である選択肢(4)や(5)は不適切だと判断できます。

上記を踏まえると、本問の解法は次のような流れで考えることができます。

1. 銅損の式から電機子抵抗R_a[Ω]を計算する
2. 電機子電圧と逆起電力の関係式から、負荷時の逆起電力E[V]を計算する
3. 逆起電力と回転数の比例関係を利用して、負荷時の回転数を計算する

まず、問題文より、銅損P_lossは3[W]で、電機子電流I_aは2[A]です。よって、電機子抵抗R_a[Ω]は次のように計算することができます。

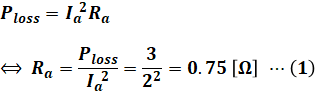
次に、逆起電力E[V]は、電機子電圧V[V]から銅損による電圧降下V_a[V]を引いた値となります。電機子電圧は問題文より12[V]なので、逆起電力E[V]は次式のように求めることができます。

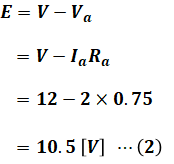
ここで、直流電動機では逆起電力は回転数に比例するため、無負荷時と負荷時の回転数の比は、そのまま逆起電力の比となります。

• n₀、n：無負荷時または負荷時の回転数 [min^－1]
• E₀、E：無負荷時または負荷時の逆起電力 [V]

(3)式において、無負荷時の逆起電力E₀は電機子電圧V＝12[V]となります。これは、無負荷の場合は(2)式での電機子電流I_aが0[A]だからです。

よって、求めたい負荷時の回転数n[min^－1]は、次のような計算によって算出することができます。

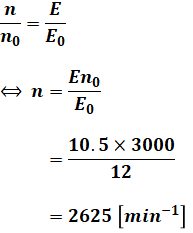
以上から、正解は(2)となります。