電験三種 R4年度下期 法規 問13 問題と解説

　問 題　　　　　

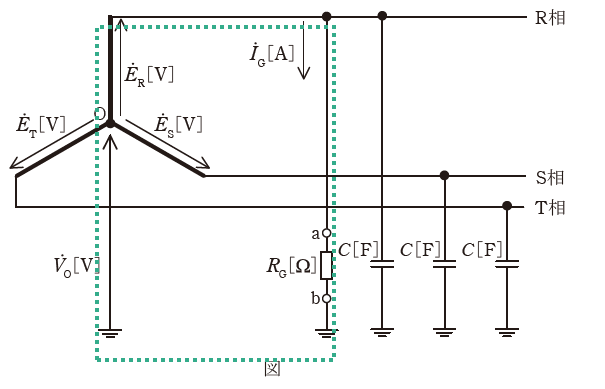
図に示すような、相電圧、角周波数ω[rad/s]の対称三相3線式高圧電路があり、変圧器の中性点は非接地方式とする。電路の一相当たりの対地静電容量をC[F]とする。

この電路のR相のみが絶縁抵抗値R_G[Ω]に低下した。このとき、次の(a)及び(b)の問に答えよ。

ただし、上記以外のインピーダンスは無視するものとする。

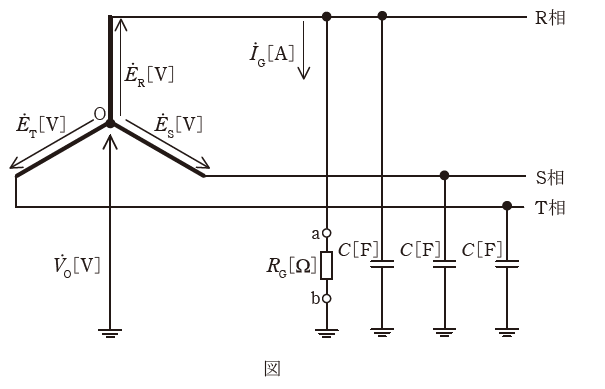
(a)　次の文章は、絶縁抵抗R_G[Ω]を流れる電流[A]を求める記述である。

R_Gを取り除いた場合

a－b間の電圧＝(　ア　)

a－b間より見たインピーダンスは、変圧器の内部インピーダンスを無視すれば、＝(　イ　)となる。

ゆえに、R_Gを接続したとき、R_Gに流れる電流は、次式となる。

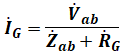＝(　ウ　)

上記の記述中の空白箇所(ア)～(ウ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

(b)　次の文章は、変圧器の中性点O点に現れる電圧[V]を求める記述である。

＝(　エ　)＋

ゆえに＝(　オ　)

上記の記述中の空白箇所(エ)及び(オ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

 

 

 

 

 

　解 説　　　　

(a)

(　ア　)に関して、ここではR_Gを取り除く(＝開放する)場合を考えるように指定されています。これはつまり、地絡事故などが起こっていない通常時の対称三相3線式の回路といえます。

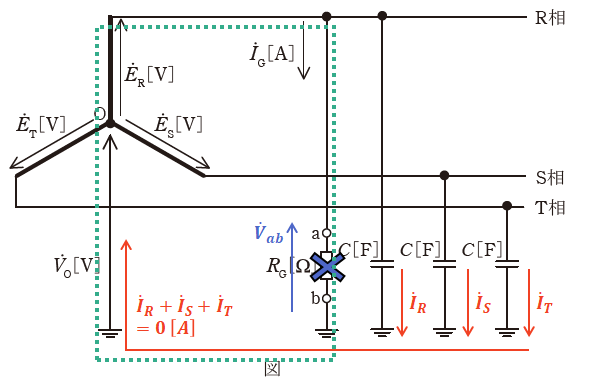
このときは上図のように、各相から大地へ流れる電流は同じ大きさで、位相が120°ずつ異なっているので、その合成電流は3つの電流が相殺しあって0[A]となります。よって、大地から中性点に流れる電流はない(＝0[A])であるため、中性点の対地電圧V_oも0[V]となります。

よって、上図緑枠の回路について電圧の大きさを考えると、以下の式が成り立ちます。

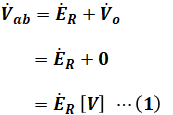
そのため、(　ア　)は「」となります。

次に(　イ　)について、a－b間から見れば、3つの対地静電容量C[F]は並列に並んでいることがわかります。よって、静電容量の合成インピーダンスは、並列接続のときはそれぞれの静電容量の和で求めることができるので、インピーダンスは次のように計算できます。

そのため、(　イ　)は「」となります。

続いて(　ウ　)について、この文章では鳳・テブナンの定理を使って式を立てているのですが、すでに問題文で式が与えられているため、この式に(　ア　)と(　イ　)の結果を代入して、以下のように計算すればよいだけです。

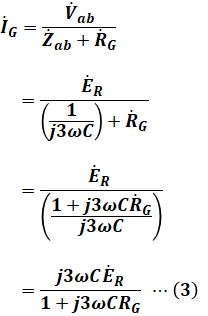
そのため、(　ウ　)は「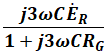」となります。

もし鳳・テブナンの定理についてしっかり学んでおきたいという場合には、鳳・テブナンの定理(基礎)や鳳・テブナンの定理(実践)のページを参照してください。

以上から、(　ア　)は「」、(　イ　)は「」、(　ウ　)は「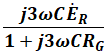」となるので、正解は(1)です。

(b)

(　エ　)に関して、ここでは中性点の対地電圧V_oや抵抗R_Gを含む式が書かれているので、下図の緑枠部分で成り立つ等式を考えます。

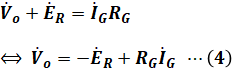
よって、(　エ　)には「」が入ります。

(　オ　)については、上記の(4)式に、設問(a)で求めた(3)式の結果を代入することで算出することができます。

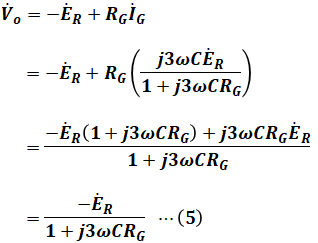
よって、(　オ　)は「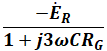」となります。

以上から、(　エ　)は「」、(　オ　)は「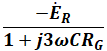」となるので、正解は(1)です。