電験三種 R4年度上期 理論 問6 問題と解説

　問 題　　　　　

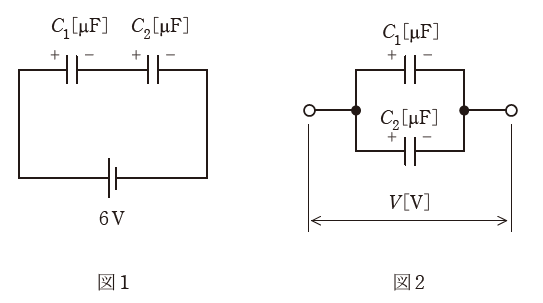
図1に示すように、静電容量C₁＝4μFとC₂＝2μFの二つのコンデンサが直列に接続され、直流電圧6Vで充電されている。次に電荷が蓄積されたこの二つのコンデンサを直流電源から切り離し、電荷を保持したまま同じ極性の端子同士を図2に示すように並列に接続する。

並列に接続後のコンデンサの端子間電圧の大きさV[V]の値として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 2/3
2. 4/3
3. 8/3
4. 16/3
5. 32/3

 

 

 

 

 

　解 説　　　　

まず、電荷Q[C]と静電容量C[F]と電圧V[V]の関係は

となりますが、図1のように直列に並んだコンデンサは電荷Qが等しいので、2つの静電容量が4：2=2：1であれば、電圧は逆に1：2になります。よって、回路全体の電圧が6[V]なので、下図のように左側のコンデンサの端子電圧が2[V]、右側のコンデンサの端子電圧が4[V]となります。

また、上図より、各コンデンサに蓄えられてる電荷Qは(1)式を使って次のように計算できます。くり返しますが、直列に並んだコンデンサの電荷Qは等しいので、この計算はどちらか一方のコンデンサで行なえば十分です。

上式と問題文より、2つのコンデンサはそれぞれ8[μC]の電荷を蓄えた状態で、図2のような並列回路に変わります。

ここで、並列に並んでいるコンデンサの合成静電容量C’は、各々の静電容量の和で表すことができます。よって、図2における合成静電容量C’は次のように計算できます。

また、(2)式より2つのコンデンサはそれぞれ8[μC]の電荷を蓄えていたので、この回路に存在する電荷は合わせて16[μC]です。よって、図2の回路全体の電圧V[V]は以下のように算出できます。

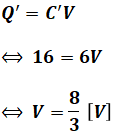
以上から、正解は(3)となります。