電験三種 R4年度上期 理論 問4 問題と解説

　問 題　　　　　

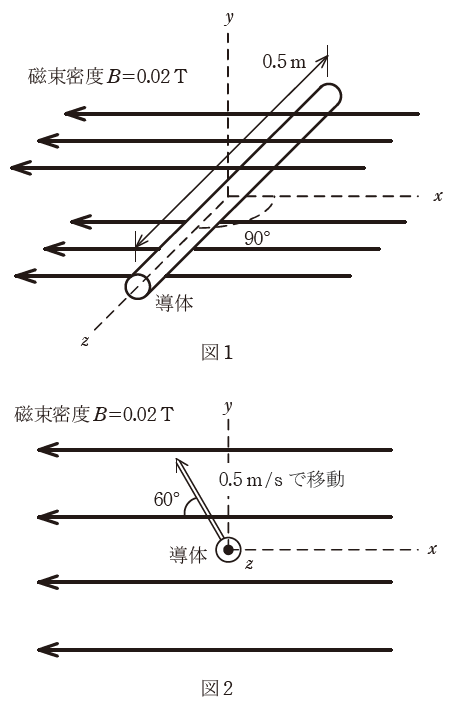
図1のように、磁束密度B＝0.02Tの一様な磁界の中に長さ0.5mの直線状導体が磁界の方向と直角に置かれている。

図2のようにこの導体が磁界と直角を維持しつつ磁界に対して60°の角度で、二重線の矢印の方向に0.5m/sの速さで移動しているとき、導体に生じる誘導起電力eの値[mV]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、静止した座標系から見て、ローレンツ力による起電力が発生しているものとする。

1. 2.5
2. 3.0
3. 4.3
4. 5.0
5. 8.6

 

 

 

 

 

　解 説　　　　

導体が磁束と直交して移動する速度をv[m/s]、磁束密度をB[T]、速度・磁束と直交する導体の長さをl[m]とすると、1本の導体に生じる誘導起電力e[V]は次式で表されます。

ここで、問題文よりB＝0.02[T]と導体の長さl＝0.5[m]は与えられていますが、速度については注意が必要で、0.5[m/s]という値をそのまま使うことができません。

(1)式におけるv、B、lは互いに直交している必要がありますが、問題文と図2によると、速度は磁界に対して60°の向きとなっています。そのため、次に示すように垂直成分の速度を計算しなければなりません。

以上から、問題文で与えられた数値と(2)式を(1)式に代入して計算を進めると、求めたい誘導起電力eの値が得られます。

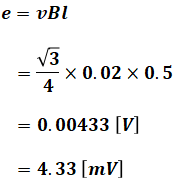
よって、正解は(3)となります。