電験三種 R4年度上期 機械 問18 問題と解説

　問 題　　　　　

以下の論理回路について、次の(a)及び(b)の問に答えよ。

(a)　図1に示す論理回路の真理値表として、正しいものを次の(1)～(5)のうちから一つ選べ。

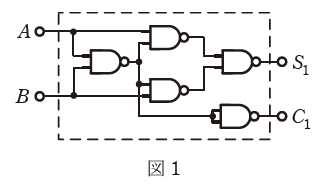
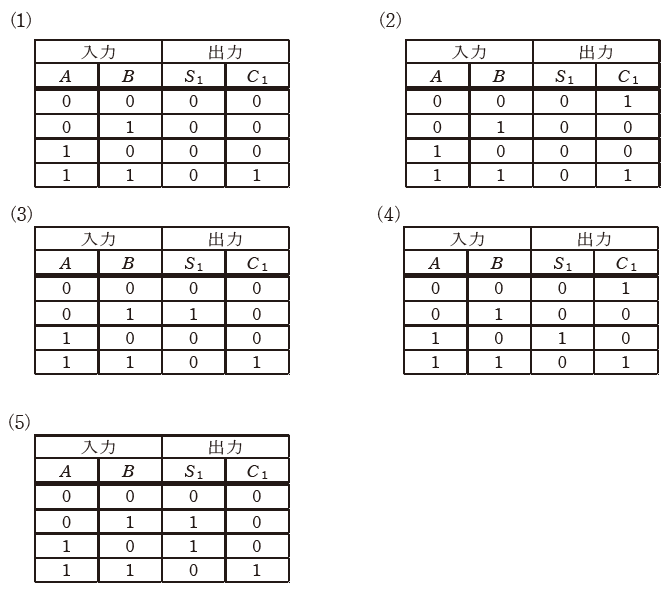
(b)　図1に示す論理回路を2組用いて図2に示すように接続して構成したとき、A、B及びC₀の入力に対する出力S₂及びC₂の記述として、正しいものを次の(1)～(5)のうちから一つ選べ。

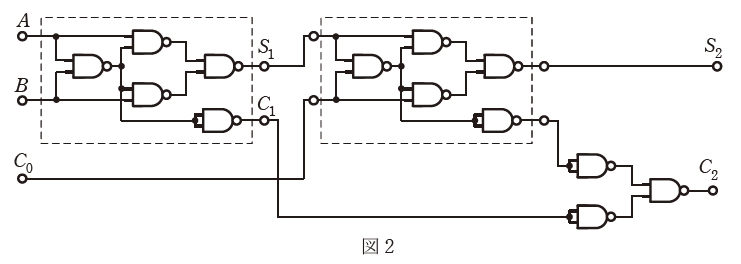
1. A＝0、B＝0、C₀＝0を入力したときの出力は、S₂＝0、C₂＝1である。
2. A＝0、B＝1、C₀＝0を入力したときの出力は、S₂＝1、C₂＝0である。
3. A＝1、B＝0、C₀＝0を入力したときの出力は、S₂＝0、C₂＝1である。
4. A＝1、B＝0、C₀＝1を入力したときの出力は、S₂＝1、C₂＝0である。
5. A＝1、B＝1、C₀＝1を入力したときの出力は、S₂＝0、C₂＝1である。

 

 

 

 

 

　解 説　　　　

(a)

まず最初に確認しておきたいのが、本問の論理回路に出てくる記号のルールの確認です。

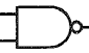
上図のように「AND」の出力側に「○」が付いているものを「NAND」といい、これは「AND」と「NOT」を合わせたものとなります。考え方として、まずは「AND」と同様に考えて、その出力結果を反対に(「NOT」に)するというものです。つまり、出力の結果は「AND」のときと真逆になります。

(入力①、入力②、出力)=(0，0，1)、(0，1，1)、(1，0，1)、(1，1，0)

以上を踏まえて、本問の解説をしていきます。

この手の問題は、具体的な入力信号を入れたときの出力を調べ、それに合う選択肢を絞っていけば、そのうち答えが出ます。今回の問題でいえば、たとえば入力を(A,B)=(0,0)として論理回路を追っていくと、次の図のように表すことができます。

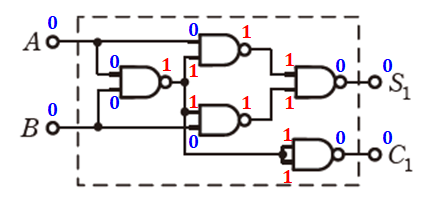
上図より、入力が(A,B)=(0,0)とき、出力は(S₁,C₁)=(0,0)になるので、選択肢(1)、(3)、(5)が残ります。

続いて別の入力を行いますが、このとき、選択肢(1)、(3)、(5)の出力結果が全部同じでは意味がないので、それは避けて入力を選んでください。たとえば(A,B)=(0,1)として論理回路を追っていくと、以下のように出力は(S₁,C₁)=(1,0)になるので、選択肢(3)、(5)が残ります。

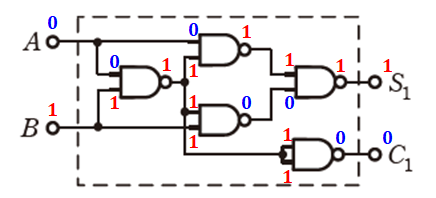
あとは2択なので、最後に(A,B)=(1,0)として論理回路を追っていくと、以下のように出力は(S₁,C₁)=(1,0)となります。

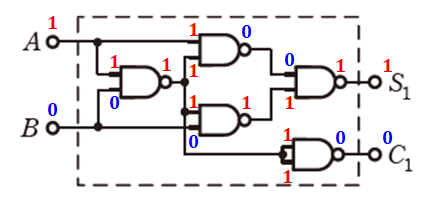
よって、選択肢(5)が正解であると判断できます。

なお、別解として、代入法ではなく真理値表を使った方法で解くこともできます。そのやり方については、類題であるH28年 問18の解説で紹介しているので、必要に応じて参照し、ご自分に合った解法を採用してください。

(b)

設問(b)でも設問(a)と同じような代入法で解くことができます。ただし、図2の枠線内は図1と全く同じ形をしているため、枠線内の構造はいちいち考えずに、設問(a)の選択肢(5)の真理値表を使うと楽です。

選択肢(1)で、入力を(A,B,C)=(0,0,0)とすると、下図のように出力は(S₂,C₂)=(0,0)となります。よって、(1)は誤りです。

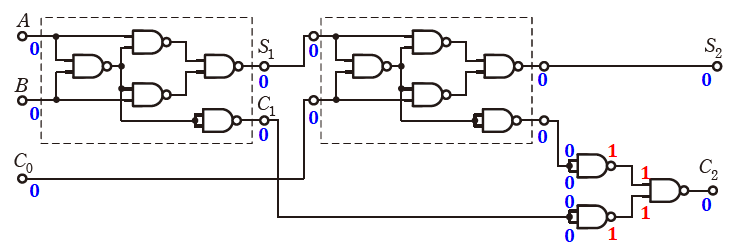
選択肢(2)で、入力を(A,B,C)=(0,1,0)とすると、下図のように出力は(S₂,C₂)=(1,0)となります。よって、(2)は正しいです。

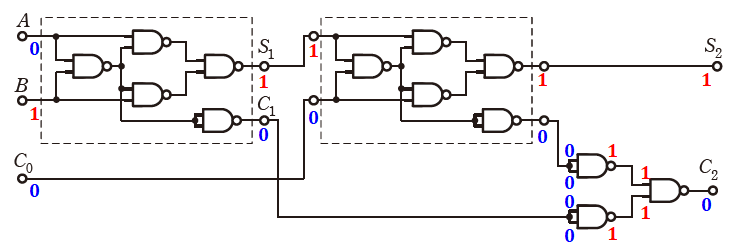
選択肢(3)で、入力を(A,B,C)=(1,0,0)とすると、下図のように出力は(S₂,C₂)=(1,0)となります。よって、(3)は誤りです。

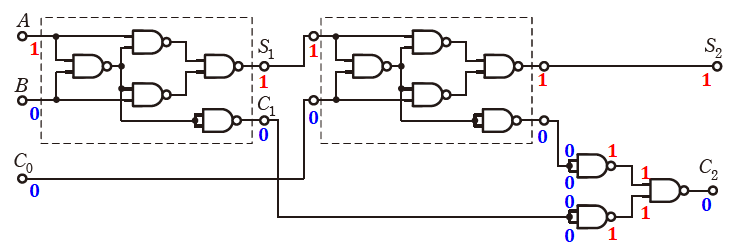
選択肢(4)で、入力を(A,B,C)=(1,0,1)とすると、下図のように出力は(S₂,C₂)=(0,1)となります。よって、(4)は誤りです。

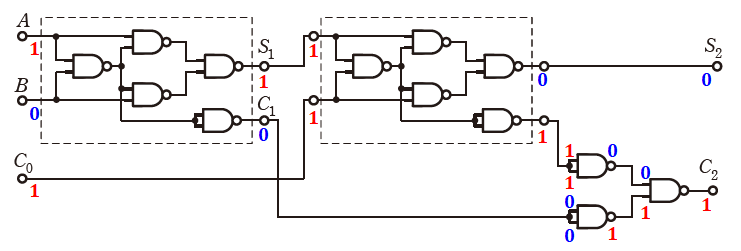
選択肢(5)で、入力を(A,B,C)=(1,1,1)とすると、下図のように出力は(S₂,C₂)=(1,1)となります。よって、(5)は誤りです。

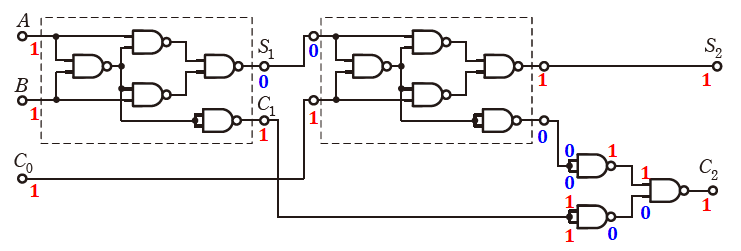
以上から、正解は(2)となります。

なお、別解として、代入法ではなく論理式を使った方法で解くこともできます。そのやり方については、類題であるH28年 問18の解説で紹介しているので、必要に応じて参照し、ご自分に合った解法を採用してください。