電験三種 R3年 理論 問14 問題と解説

　問 題　　　　　

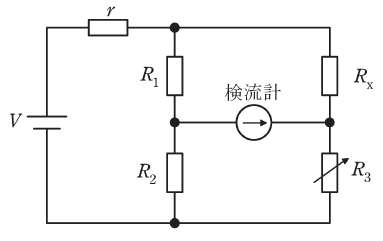
図のブリッジ回路を用いて、未知の抵抗の値R_X[Ω]を推定したい。可変抵抗R₃を調整して、検流計に電流が流れない状態を探し、平衡条件を満足するR_X[Ω]の値を求める。

求めた値が真値と異なる原因が、R_k(k＝1、2、3)の真値からの誤差ΔR_kのみである場合を考え、それらの誤差率ε_k＝ΔR_k/R_kが次の値であったとき、R_Xの誤差率として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ε₁＝0.01、ε₂＝－0.01、ε₃＝0.02

1. 0.0001
2. 0.01
3. 0.02
4. 0.03
5. 0.04

 

 

 

 

 

　解 説　　　　

ブリッジ回路において、真ん中の抵抗(今回は検流計)に電流が流れないとき、このブリッジ回路は「平衡状態にある」と表現されます。平衡状態にあるときには、真ん中以外の4つの抵抗のうち、2組の対角線上の抵抗の積が等しくなります。

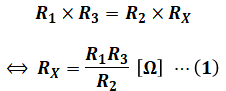
続いて誤差率について考えます。誤差ΔR_kは問題文にもある通り、「測定値R_k測から真値R_k真を引いた値」となります。また、これも問題文にありますが、誤差率はε_k＝ΔR_k/R_k真と表されるので、次のような等式が成り立ちます。

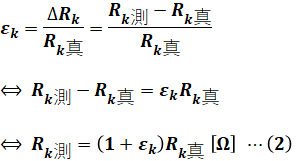
R₁、R₂、R₃の誤差率はそれぞれε₁＝0.01、ε₂＝－0.01、ε₃＝0.02と与えられているので、これを(2)式に代入すると、(3)～(5)式のように計算できます。

最終的に求めたいのはR_Xの誤差率ε_Xですが、そのためには真値R_X真と測定値R_X測を式で表す必要があります。

真値R_X真は、(1)式より次のようになります。

測定値R_X測は、(1)式と(3)～(5)式を合わせ、さらに(6)式を使うことで、次のように計算できます。

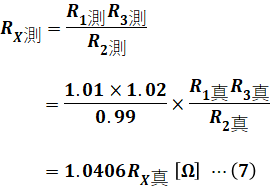
よって、誤差率の式ε_k＝ΔR_k/R_k真と(7)式を使って以下のように計算すると、誤差率ε_Xを求めることができます。

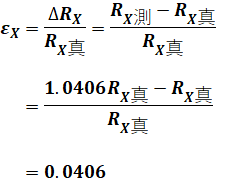
以上から、正解は(5)です。