問 題
図のように、x方向の平等電界E[V/m]、y方向の平等磁界H[A/m]が存在する真空の空間において、電荷-e[C]、質量m[kg]をもつ電子がz方向の初速度v[m/s]で放出された。
この電子が等速直線運動をするとき、vを表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、真空の誘電率をε0[F/m]、真空の透磁率をμ0[H/m]とし、重力の影響を無視する。
また、電子の質量は変化しないものとする。図中の⦿は紙面に垂直かつ手前の向きを表す。
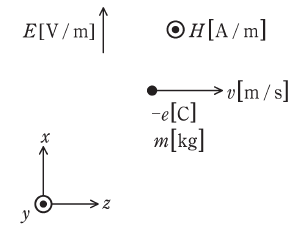
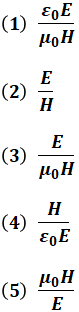
解 説
問題文を読むと、電子が最初にz方向へ初速度v[m/s]で放出されたあと、そのまま等速直線運動を続けていることがわかります。加速も減速も方向転換もしないということは、この電子には一切何の力も働いていないことになります。
実際には、ここには電界も磁界も存在するため、電子は電界や磁界から力を受けているはずです。それでも等速直線運動を続けるのは、電子が電界と磁界のそれぞれから受ける力がつり合っている(向きが反対で大きさが等しい)からです。
よって、解法のアプローチとして、電子が電界から受ける力と磁界から受ける力を式で表し、それらの大きさをイコールで結ぶことでvを求めていこうと思います。
電子が電界から受ける力(静電気力)F電界は、以下に示す運動方程式で表すことができます。
![]()
- F電界:静電気力 [N]
- m0:電子の質量 [kg]
- a:電子の加速度 [m/s2]
- e:電子の電荷 [C]
- E:電界 [V/m]
また、静電気力の向きは電界の向きと反対(画面下向き)となります。
一方、磁界の中を運動する電子が受ける電磁力のことをローレンツ力といいますが、ローレンツ力F磁界は下式で表すことができます。
![]()
- F磁界:ローレンツ力 [N]
- B:磁束密度[T]
- e:電子の電荷[C]
- v:電子の速度[m/s]
また、上記のB、e、vのそれぞれの向きは、フレミングの左手の法則に従います。つまり、左手の親指と人差し指と中指を互いに直交させたとき、指の向きと電流、磁界、電磁力とが以下のように対応します。
- 中指:電流の向き(電子の速度の反対向き)
- 人差し指:磁界の向き
- 親指:電磁力の向き
今回の場合、電流は電子と反対なので画面左向き、磁界は画面奥から手前向きなので、上記より電磁力(ローレンツ力)は画面上向きとなることがわかります。
以上より、画面下向きの静電気力F電界と、画面上向きのローレンツ力F磁界の大きさが等しくなるようなvを求めたいので、(1)式と(2)式を使って次のように計算します。
![]()
これを答えにしたいところですが、選択肢を見ても当てはまるものがありません。分母のEはそのまま使えそうですが、分子のBが選択肢にないため、これをほかのパラメータに変換する必要があります。
ここで、磁束密度B[T]は、(真空または空気中の)透磁率μ0[H/m]と磁界の強さH[A/m]の積で表すことができます。
![]()
よって、(4)式を(3)式に代入することで、求めるvを選択肢に合うパラメータで表すことができます。
![]()
以上から、正解は(3)となります。

コメント