問 題
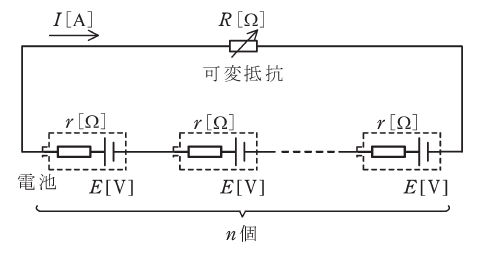
図のように、起電力E[V]、内部抵抗r[Ω]の電池n個と可変抵抗R[Ω]を直列に接続した回路がある。この回路において、可変抵抗R[Ω]で消費される電力が最大になるようにその値[Ω]を調整した。
このとき、回路に流れる電流Iの値[A]を表す式として、正しいものを次の(1)~(5)のうちから一つ選べ。
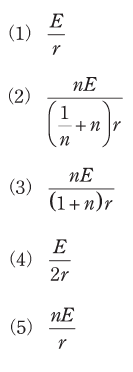
解 説
問題の図には複数個の電池が並んでいますが、これらは直列接続なので、まとめると下図のような回路図となります。
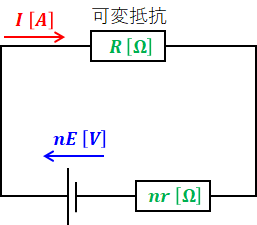
ここで、可変抵抗R[Ω]で消費される電力が最大になるのは、可変抵抗R[Ω]がそれ以外の合成抵抗(今回はnr[Ω])と同じになるときです。つまり、下式のように表すことができます。
![]()
上記より、電流I[A]は次のように計算することができます。
![]()
よって、正解は(4)となります。
ただし、出題頻度から見て、上記の法則は必ずしも重要とはいえません。これを知らない場合の解法を以下に示します。
まず、今回は可変抵抗での電力Pを最大にしたいのですが、解説の冒頭で示した回路図より、電力Pは次のように表されます。
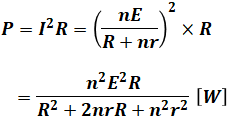
上式のままでは分母・分子ともに変数Rが含まれていて、どうしたらPが最大になるのかわかりづらいです。よって、分母・分子それぞれをRで割って、分子から変数Rを消します。
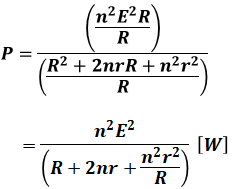
n、E、rは全て定数なので、上式の分子は定数であり、Pを最大にするには分母を最小にすればよいことがわかります。さらにいえば、分母の2nrは定数なので、残りの2項(Rとn2r2/R)の和が最小になるようなRを考えることになります。
ここで、「変数xと変数yの積(xy)が一定であるならば、x=yのときにその和(x+y)が最小になる」という法則があります。これを「最小の定理」といいます。
余談ですが、「変数xと変数yの和(x+y)が一定であるならば、x=yのときにその積(xy)が最大になる」という法則もあります。これを「最大の定理」といいます。
話を少し戻して、今回は「R」と「n2r2/R」の2項の和を最小にしたいのですが、これらの積は定数であることがわかります。
![]()
よって、最小の定理より、積が定数ならこれら2項が同じ値を取るときに、その積は最小値となります。
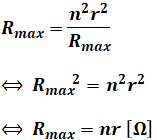
あとは最初の解法と同様、電流I[A]を次のように計算できます。
![]()
以上から、正解は(4)となります。

コメント