電験三種 R3年 理論 問2 問題と解説

　問 題　　　　　

二つの導体小球がそれぞれ電荷を帯びており、真空中で十分な距離を隔てて保持されている。

ここで、真空の空間を、比誘電率2の絶縁体の液体で満たしたとき、小球の間に作用する静電力に関する記述として、正しいものを次の(1)～(5)のうちから一つ選べ。

1. 液体で満たすことで静電力の向きも大きさも変わらない。
2. 液体で満たすことで静電力の向きは変わらず、大きさは2倍になる。
3. 液体で満たすことで静電力の向きは変わらず、大きさは1/2倍になる。
4. 液体で満たすことで静電力の向きは変わらず、大きさは1/4倍になる。
5. 液体で満たすことで静電力の向きは逆になり、大きさは変わらない。

 

 

 

 

 

　解 説　　　　

二つの導体小球がそれぞれ正電荷を帯びているのか負電荷を帯びているのか書かれていませんが、両者が同じなら静電力は斥力(反発し合う力)となり、両者の正負が異なるなら静電力は引力となります。

本問では「真空の空間」だったものが「比誘電率2の絶縁体の液体で満たした」状態に変わりますが、電荷の正負が入れ替わるような条件はないので、液体で満たすことで静電力の向きが変わることはありません。よって、この時点で(5)は不適です。

ここで、2つの点電荷(導体小球)の間にはたらく静電気力は以下の式で示されます。

• F：静電気力 [N]
• ε₀：真空の誘電率　8.854×10^-12 [F/m]
• Q：電荷 [C]
• r：電荷間の距離 [m]

また、真空ではなく比誘電率ε_rの条件下だと、2つの点電荷(導体小球)の間にはたらく静電気力は以下の式で示されます。

よって、今回の場合、小球の間に作用する静電力の大きさは次のように変化します。

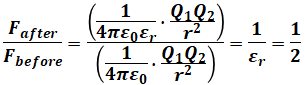
以上から、液体で満たすことで静電力の向きは変わらず、大きさは1/2倍になるので、正解は(3)です。