問 題
2進数、10進数、16進数に関する記述として、誤っているものを次の(1)~(5)のうちから一つ選べ。
- 16進数の(6)16を16倍すると(60)16になる。
- 2進数の(1010101)2と16進数の(57)16を比較すると(57)16の方が大きい。
- 2進数の(1011)2を10進数に変換すると(11)10になる。
- 10進数の(12)10を16進数に変換すると(C)16になる。
- 16進数の(3D)16を2進数に変換すると(111011)2になる。
正解 (5)
解 説
各選択肢について、2進数や16進数のままでは計算しにくいので、ここでは全ての数値を10進数に直してから考えていきます。
(1)に関して、16進数は、1桁が以下の16種類で構成されます。
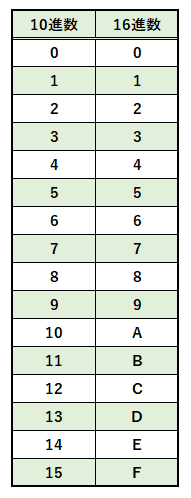
上表より、(6)16=(6)10です。これを16倍すると、(6)10×16=(96)10となります。今度はこれを16進数に戻します。
10進数の数を16進数に変換したい場合、下図のようにどんどん16で割っていって、その余りに注目します。最初は96÷6=6で余り「0」、次は6÷16=0で余り「6」となり、この余りを最後のほうから最初のほうへと読んでいったのが16進数の数です。
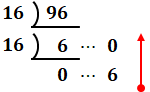
よって、(96)10=(60)16なので、(1)は正しいです。
(2)に関して、(1010101)2と(57)16をそれぞれ10進数で表すと、下図のようになります。
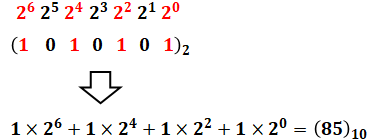
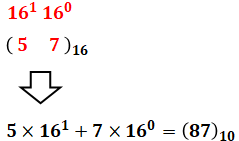
よって、(57)16のほうが大きいので、(2)は正しいです。
(3)に関して、(1011)2を10進数で表すと下図のようになるので、(3)は正しいです。
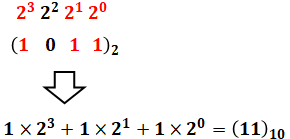
(4)に関して、(1)の解説で示した図を見ると、(12)10=(C)16であることがわかります。よって、(4)は正しいです。
(5)に関して、まずは(3D)16を10進数に直します。
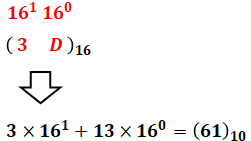
続いて、(3D)16=(61)10を10進数に直します。
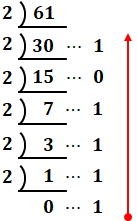
上図より、(3D)16=(61)10=(111101)2となるので、(5)の記述が誤りであると判断できます。
以上から、正解は(5)です。

コメント