問 題
次の文章は、図に示す抵抗R、並びにキャパシタCで構成された一次遅れ要素に関する記述である。
図の回路において、入力電圧に対する出力電圧を、一次遅れ要素の周波数伝達関数として表したとき、折れ点角周波数ωcは( ア )rad/sである。
ゲイン特性は、ωcよりも十分低い角周波数ではほぼ一定の( イ )dBであり、ωcよりも十分高い角周波数では、角周波数が10倍になるごとに( ウ )dB減少する直線となる。
また、位相特性は、ωcよりも十分高い角周波数でほぼ一定の( エ )°の遅れとなる。
上記の記述中の空白箇所(ア)~(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
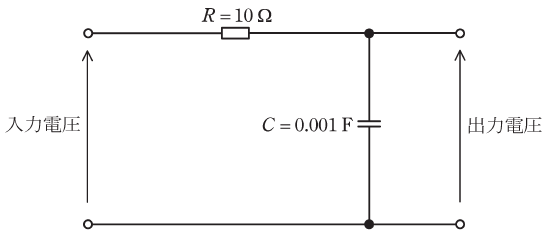
- ア イ ウ エ
- 100 20 10 45
- 100 0 20 90
- 100 0 20 45
- 0.01 0 10 90
- 0.01 20 20 45
解 説
伝達関数の問題は頻出ですが、今回は問題文で与えられる情報が少なく、自力で折れ点角周波数ωCやゲイン特性の式を組み立てなくてはなりません。よって、ハイレベルな内容となっているため、個人的にはこの問題を捨て問題としてしまっても構わないと思います。
まず、問題文の初めのほうに「図の回路において、入力電圧に対する出力電圧を、一次遅れ要素の周波数伝達関数として表したとき」とあるので、この伝達関数を式にするのが当面の目標となります。
図のうち入力電圧に注目すると、RとCが直列に並んでいるため、入力電圧Ei(jω)は、電流I(jω)を使って次のように表すことができます。
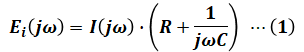
一方、出力電圧に注目すると、こちらにはCしかないため、出力電圧Eo(jω)は、電流I(jω)を使って次のように表されます。
![]()
(1)式と(2)式から、出力電圧Eo(jω)と入力電圧Ei(jω)の関係式は以下のようになります。
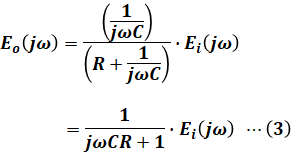
よって、周波数伝達関数G(jω)の式は次の(4)式のように計算できます。
![]()
ここで、RC直列回路における時定数τの式は、以下のように表すことができます。
![]()
(5)式を(4)式に代入したのが、以下の(6)式です。
![]()
これで伝達関数G(jω)を式で表すことが一応できたので、続いて問題文に書かれている「ゲイン特性」を計算していきます。ゲイン特性は以下の(7)式で表されます。これはゲイン特性の定義となる式です。
![]()
すでに(6)式でG(jω)は具体的になっていますが、(7)式ではこれが絶対値に挟まれています。そのため、まずは虚数を含む絶対値の計算によって、|G(jω)|を求めます。
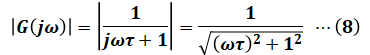
続いて(8)式を(7)式に代入して、計算できるところまで進めます。
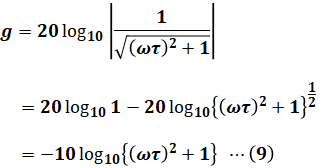
以上で伝達関数G(jω)とゲイン特性gの式が大体見えてきたので、ここから具体的に設問の穴埋めをしていきたいと思います。
( ア )について、折れ点角周波数ωcとは、ωが時定数の逆数(ω=1/τ)のときのωのことです。よって、以下のように計算することができます。
![]()
(10)式より、( ア )には「100」が入ります。
( イ )で、ωがωc(=1/τ)よりも十分に低いということは、ωTが1よりも十分に小さい(ωτ≪1)ということと同義です。よって、(9)式は次のように近似できます。
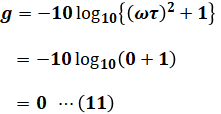
(11)式より、( イ )には「0」が入ります。
( ウ )で、ωがωc(=1/τ)よりも十分に高いということは、ωTが1よりも十分に大きい(ωτ≫1)ということと同義です。よって、(9)式は次のように近似できます。
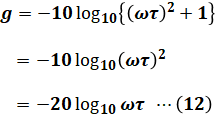
(12)式でωが10倍になると、ゲイン特性gは次のg’のように変化します。
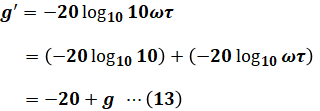
(13)式より、ωが10倍になるごとにgは20dBずつ減少していくことがわかるので、( ウ )には「20」が入ります。
( エ )について、位相角θは次の式で表されます。ただし、これは電験三種のレベルからするとマニアックな知識だと感じるので、余裕のない方は無理に覚えなくていいと思います。
![]()
tan-1(アークタンジェント)のままだと考えにくいので、これをtan(タンジェント)の式に直します。
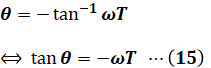
(15)式より、ωが十分に高いときには、tanθ=-∞となることがわかります。tanθ=-∞のときのθは-90°なので、これは90°の遅れを意味します。
よって、( エ )には「90」が入ります。
以上から、( ア )が「100」、( イ )が「0」、( ウ )が「20」、( エ )が「90」となるので、正解は(2)です。

コメント