問 題
次の文章は、三相同期電動機に関する記述である。
三相同期電動機が負荷を担って回転しているとき、回転子磁極の位置と、固定子の三相巻線によって生じる回転磁界の位置との間には、トルクに応じた角度δ[rad]が発生する。この角度δを( ア )という。
回転子が円筒形で2極の三相同期電動機の場合、トルクT[N・m]はδが( イ )[rad]のときに最大値になる。さらにδが大きくなると、トルクは減少して電動機は停止する。同期電動機が停止しない最大トルクを( ウ )という。
また、同期電動機の負荷が急変すると、δが変化し、新たなるδ’に落ち着こうとするが、回転子の慣性のために、δ’を中心として周期的に変動する。これを( エ )といい、電源の電圧や周波数が変動した場合にも生じる。
( エ )を抑制するには、始動巻線も兼ねる( オ )を設けたり、はずみ車を取り付けたりする。
上記の記述中の空白箇所(ア)~(オ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
- ア イ ウ エ オ
- 負荷角 π 脱出トルク 乱調 界磁巻線
- 力率角 π 制動トルク 同期外れ 界磁巻線
- 負荷角 π/2 脱出トルク 乱調 界磁巻線
- 力率角 π/2 制動トルク 同期外れ 制動巻線
- 負荷角 π/2 脱出トルク 乱調 制動巻線
解 説
( ア )には「負荷角」か「力率角」が入りますが、力率角はその言葉からもわかるように、電力Pに関係する角度θで、電圧Vと電流Iの間の角度を指します(P=VIcosθ)。
一方の負荷角は、界磁単独の磁束と電機子反作用を考慮した電機子磁束との位相差のことです。蛇足ですが、内部誘導起電力Eoと電機子端子電圧Vの位相差と表現されることもあります。いずれも同じ意味で、記号で表すとδです。
よって、( ア )には「負荷角」を入れるのが適切です。
( イ )で、三相同期電動機のトルクTは以下の式で表されます。
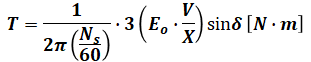
- T:トルク [N・m]
- Ns:同期速度 [min-1]
- Eo:内部誘導起電力 [V] (相電圧実効値)
- V:電機子端子電圧 [V] (相電圧実効値)
- X:同期リアクタンス [Ω]
- δ:EoとVとの位相角 [rad]
上式は、「三相同期機の出力の式」と「トルクと出力の関係式」から導くことができます。詳細な導出を知りたい場合には、同期機の同期速度、出力、トルクのページを参照してください。
上式よりトルクTはsinδに比例するので、トルクTが最大になるのはsinδ=1のときです。よって、( イ )には「π/2」が入ると判断できます。
( ウ )で、δ=π/2のときにsinδ=1となり、トルクは最大となります。これよりもδが大きくなるとsinδは小さくなっていき、いつかは同期電動機が同期できずに停止してしまいます。
このように同期状態から外れることを「同期外れ」といい、同期状態から外れるときのトルクを「脱出トルク」といいます。よって、( ウ )は「脱出トルク」となります。
( エ )の選択肢には「乱調」と「同期外れ」がありますが、同期外れは( ウ )で解説した通り、同期電動機のトルクが脱出トルクを下回り、同期できなくなって停止することを指す用語です。よって、( エ )は「同期外れ」ではないので、「乱調」が入るはずだと推測できます。
乱調の説明は問題文にある通りです。同期電動機の負荷や電源電圧、周波数のいずれかが急に変動した際、その変化に応じてδがδ’に変わるのですが、回転子の慣性のためにδはぴたりとδ’に変化できず、行き過ぎたり戻りすぎたりしながら、徐々にδ’に近づきます。
δ’を中心として周期的に変動するこの現象が「乱調」なので、( エ )にはこれが入ります。
( オ )で、制動巻線は、誘導トルクによって始動トルクを発生させ電動機を起動させるという特徴が有名ですが、同期電動機の乱調を抑える役割も果たします。
これ自体はややマイナーな知識ですが、( オ )の直前に「始動巻線も兼ねる」とあるので、これをヒントにすれば答えやすいと思います。よって、( オ )は「制動巻線」となります。
以上から、( ア )は「負荷角」、( イ )は「π/2」、( ウ )は「脱出トルク」、( エ )は「乱調」、( オ )は「制動巻線」となるので、正解は(5)です。

コメント