電験三種 R3年 電力 問2 問題と解説

　問 題　　　　　

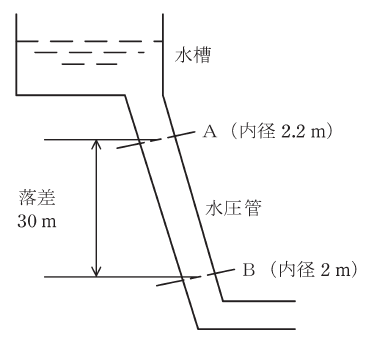
図で、水圧管内を水が充満して流れている。断面Aでは、内径2.2m、流速3m/s、圧力24kPaである。このとき、断面Aとの落差が30m、内径2mの断面Bにおける流速[m/s]と水圧[kPa]の最も近い値の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

ただし、重力加速度は9.8m/s²、水の密度は1000kg/m³、円周率は3.14とする。

• 流速[m/s]　水圧[kPa]

1. 　3.0　　　　318
2. 　3.0　　　　316
3. 　3.6　　　　316
4. 　3.6　　　　310
5. 　4.0　　　　300

 

 

 

 

 

　解 説　　　　

流水の流速や水圧が問われているので、水力学にとって重要な公式である「ベルヌーイの定理」と「連続の式」を使います。これらはどちらも重要なので、ぜひ押さえておくべき知識です。

【ベルヌーイの定理】

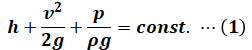
• h：基準からの高さ [m]
• v：流速 [m/s]
• p：圧力 [N/m²]＝[Pa]
• ρ：水の密度＝1000 [kg/m³]
• g：重力加速度＝9.8 [m/s²]
• const.：constantの略で「一定」という意味

これを文章で表現すると、水が管の中を流れているとき、そのうちどの点においても「位置エネルギー」と「運動エネルギー」と「圧力エネルギー」の和は一定となります。要するに、流水のエネルギー保存の法則を表しています。

【連続の式】

• A：断面積[m²]
• v：流速[m/s]

上記において、断面積と流速を掛けるとその単位は[m³/s]となり、その地点での流量が求められます。水管中をスムーズに水が流れている場合、水管中のどの断面をとってもそこを通る水の量は一定、という意味の式となります。これは、流水の質量保存の法則を表しています。

以上を踏まえて設問を解いていきます。

まず、断面Aでの内径と流速がわかっていて、断面Bでの断面もわかっているため、断面Bでの流速v_Bは(2)式を使って次のように計算できます。

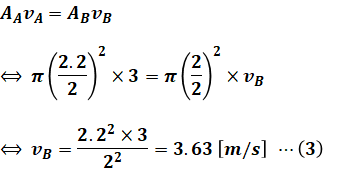
よって、1つ目の答えは「3.6」となります。

次に、断面Bでの水圧p_Bを求めたいので、(1)式を以下のように書き換え、各種の値を代入して計算していきます。

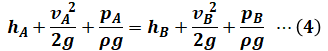
(4)式において、h_Aとh_Bは具体的に与えられていませんが、落差は30[m]なので、h_A－h_B＝30[m]であることがわかります。問題文で与えられた数値や(3)式の結果を使うと、(4)式は次のように計算できます。

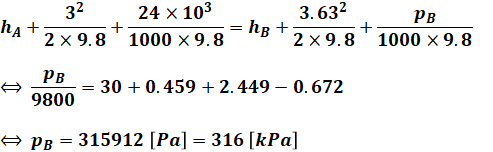
よって、2つ目の答えは「316」となります。

以上から、正解は(3)です。