電験三種 R2年 理論 問15 問題と解説

　問題　　　　　

図のように、線間電圧(実効値)200Vの対称三相交流電源に、1台の単相電力計W₁、X＝4Ωの誘導性リアクタンス3個、R＝9Ωの抵抗3個を接続した回路がある。単相電力計W₁の電流コイルはa相に接続し、電圧コイルはb－c相間に接続され、指示は正の値を示していた。

この回路について、次の(a)及び(b)の問に答えよ。

ただし、対称三相交流電源の相順は、a、b、cとし、単相電力計W₁の損失は無視できるものとする。

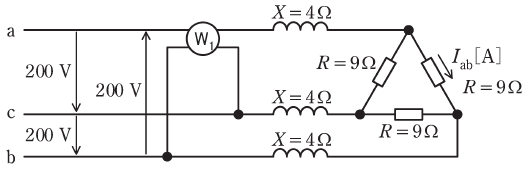
(a)　R＝9Ωの抵抗に流れる電流I_abの実効値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

(b)　単相電力計W₁の指示値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

正解 (a)-(2), (b)-(3)

　解説　　　　

問題の回路は三相回路になっていて、このままでは考えにくいので、まずは三相回路から1相分の等価回路を抜き出して考えます。この際、Δ結線では中性点がなく等価回路が描けないので、Δ結線をY結線に直した上で下図のように等価回路を描きます。

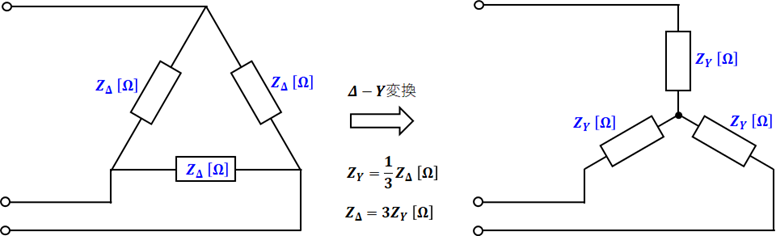
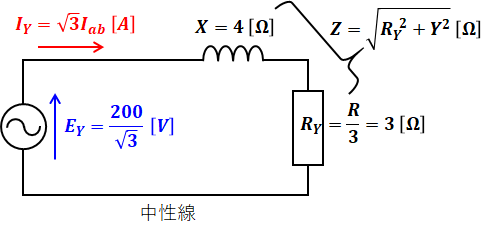
上図に示した通り、Δ-Y変換では1相あたりの抵抗の値は1/3倍となり、電流は√3倍になります。リアクタンスはΔ-Y変換に関わらないのでそのままです。また、Y結線の相電圧は線間電圧(＝Δ結線の相電圧)の1/√3倍になります。

この等価回路の合成インピーダンスをZとすると、オームの法則を使うことで次のように電流I_abを計算することができます。

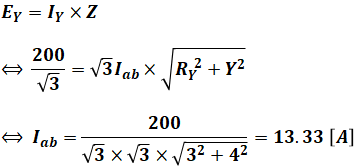
よって、正解は(2)です。

この単相電力計W₁は、電流コイルがa相に、電圧コイルはb－c相間に接続されているため、その指示値(電力)は次の式で表すことができます。

ここで、電流Iについては(a)ですでに求めています。(a)では1相あたりの等価回路を考えたので、そこを流れる電流I_Yが1相あたりの電流です。電流の大きさはa相でもb相でもc相でも一緒なので(位相は違いますが)、a相を流れる電流I[A]は次のようになります。

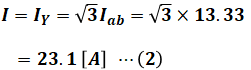
また、電圧Vも簡単にわかります。問題文には線間電圧が200[V]とあり、問題の回路図でもそのように描かれているため、b－c相間の電圧の大きさは200[V]です。

以上でIとVがわかったので、残る「IとVのなす角(位相差)」を求めるのがこの問題の肝です。

いきなりI(a相を流れる電流)とVのなす角(b－c相間の電圧)を考えるのは難しいので、最初はa相だけで考えて、a相の電流と電圧の位相差を求めることにします。

下図は(a)で使った1相あたりの等価回路です。これはコイルを含む回路なので、電流は電圧に対して遅れます(ちなみに、回路にコンデンサがあれば、電流は電圧に対して進みます)。どのくらい遅れるのかは抵抗とコイルの兼ね合いですが、これは直角三角形を描くとわかります。

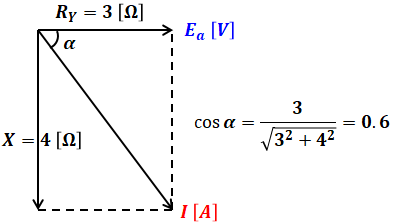
上図の通り、a相の電流Iは、a相の相電圧E_aよりもαだけ遅れることになります。

続いて、今度はa相の相電圧E_aとb－c相間の電圧Vの位相差について考えます。まずは下図を確認してください。

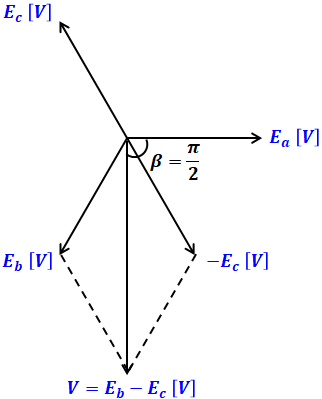
上図を描く順番としては、まずはE_aを基準として、時計回りで等間隔(120°ずつ)にE_b、E_cを描きます。E_bとE_cはそれぞれb相とc相の相電圧です。この順番は、問題文に「対称三相交流電源の相順は、a、b、c」とあるためです。

また、知りたいのはb－c相間の電圧Vの位相ですが、b－c相間の表現は文字通り「bからcを引く」で表すことができます。よって、E_cの反対である－E_cを描き、それとE_bとの合力がVになります。

ここまで描くと上図からわかるように、VはE_aに対してπ/2だけ遅れることになります。

以上の角αと角βを合わせることで、求めたいcosθを計算することができます。途中の計算では、三角関数の公式「cos(θ₁－θ₂)＝cosθ₁cosθ₂＋sinθ₁sinθ₂」を使っています。

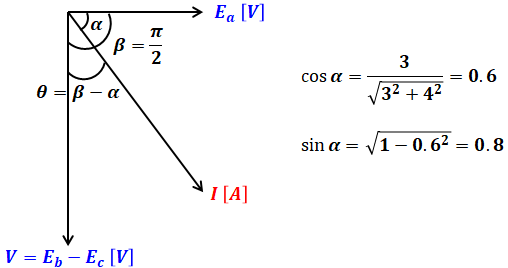
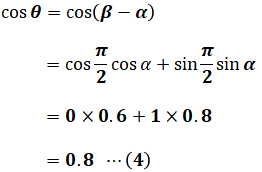
ここまで長かったですが、(2)式、(3)式、(4)式を(1)式に代入することで、問われている電力Pを求めることができます。

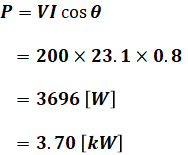
よって、正解は(3)となります。

電験三種 R2年理論問15 問題と解説