電験三種 R2年 理論 問7 問題と解説

　問 題　　　　　

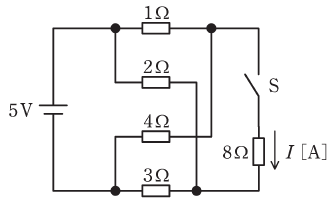
図のように、直流電源にスイッチS、抵抗5個を接続したブリッジ回路がある。この回路において、スイッチSを開いたとき、Sの両端間の電圧は1Vであった。

スイッチSを閉じたときに8Ωの抵抗に流れる電流Iの値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 0.10
2. 0.75
3. 1.0
4. 1.4
5. 2.0

 

 

 

 

 

　解 説　　　　

パッと見は複雑そうな回路図ですが、ヒントを与えてくれているのか、問題文を読むとこれがブリッジ回路であることが明言されています。そのため、まずは問題の回路図を次のような一般的なブリッジ回路図に描き直します(そのままでも構いませんが、下図のほうが考えやすいと思います)。

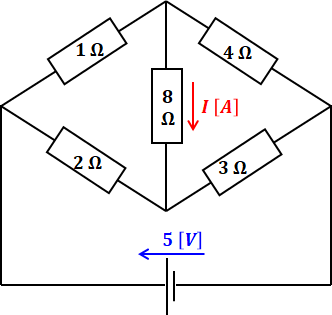
また、この問題で問われているのは、Sを閉じたときに8Ωの抵抗に流れる電流Iの値です。今回のように複雑そうな回路において、ある1箇所での電流値や電圧を求める際には「テブナンの定理」を用いるのが定石です。

テブナンの定理を使えば、目的とする抵抗以外の部分を1つの抵抗と1つの電源に置き換え、下図右側のような簡単な等価回路に変換することができます。

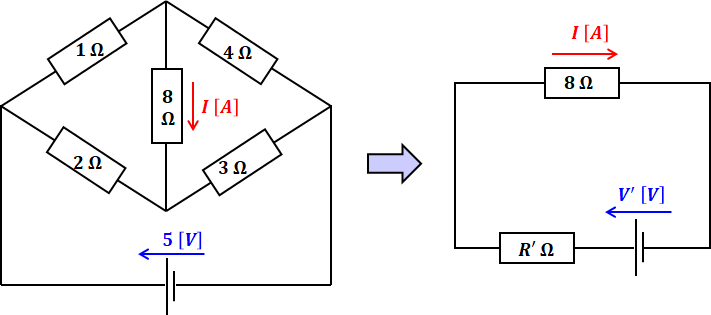
テブナンの定理の詳細な説明は鳳・テブナンの定理(実践)のページを読んでほしいのですが、簡単にまとめると以下の4ステップで構成されます。

1. 目的の抵抗の両端で断線させる
2. 1の状態で、断線させた両端の電圧差が合成電源V’となる
3. 2の状態から、全ての電圧源を短絡させる
4. 3の状態で、残った抵抗の合成抵抗がR’となる

ステップ1と2の結果を図示すると以下の図のようになります。問題文ですでに1[V]と与えられているため、ここまでは計算不要です。

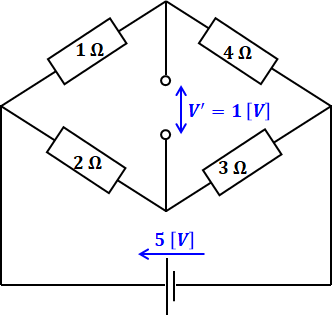
続いて、ステップ3を考えると、次のように表すことができます。

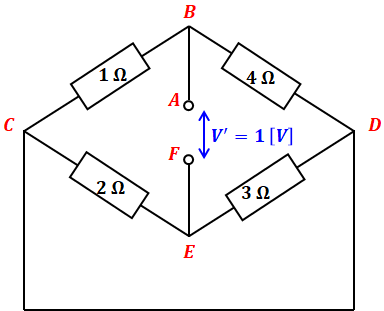
上図を見ながらステップ4について考えます。ちょっとややこしい図ですが、点Aを起点として考えると、点Bで分岐して、抵抗をはさんで点Cと点Dへ進みます。

ここで、点Cと点Dは図の下側で短絡しているため、この2点の電圧は同じです。つまり、BC間の抵抗とBD間の抵抗は並行であることがわかります。また、同じ理屈でCE間とDE間の抵抗も並行に並んでいます。そして終点の点Fに行き着きます。

これらをまとめると、この回路は1Ωと4Ωの抵抗が並行に、2Ωと3Ωの抵抗も並行に並んでいて、これら2組が直列に並んでいるため、その合成抵抗R’は次のように計算することができます。

以上でV’とR’がわかったので、問題の回路はテブナンの定理によって次のように描き換えることができます。

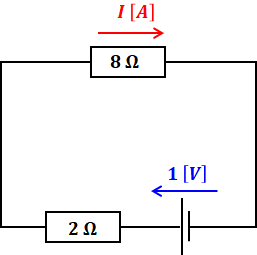
よって、求める電流Iは次のように計算することができます。

以上から、正解は(1)となります。