問 題
平等な磁束密度B0[T]のもとで、一辺の長さがh[m]の正方形ループABCDに直流電流I[A]が流れている。B0の向きは辺ABと平行である。
B0がループに及ぼす電磁力として、正しいものを次の(1)~(5)のうちから一つ選べ。
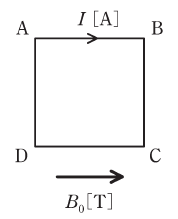
- 大きさ2IhB0[N]の力
- 大きさ4IhB0[N]の力
- 大きさIh2B0[N・m]の偶力のモーメント
- 大きさ2Ih2B0[N・m]の偶力のモーメント
- 力も偶力のモーメントも働かない
解 説
問われているのはB0がループに及ぼす電磁力なので、まずはフレミングの左手の法則を思い出してください。
フレミングの左手の法則とは、左手の親指と人差し指と中指を互いに直交させたとき、指の向きと電流I、磁界B、電磁力Fとが以下のように対応するという法則です。
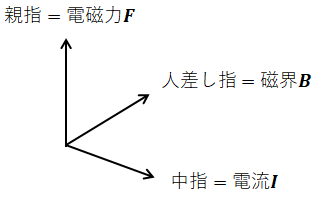
- 中指:電流Iの向き
- 人差し指:磁界Bの向き
- 親指:電磁力Fの向き
今回の場合、電流と磁界がすでに与えられているため、これら2つが垂直に交わっていれば、両方に直交する向きに電磁力が働くことになります。
ただし、電流は正方形ループを流れていて向きが一定ではないので、各辺を流れる電流に対する電磁力をそれぞれ分けて考える必要があります。そのため、以下では辺AB、辺BC、辺CD、辺DAの4パターンについて、生じる電磁力の大きさを計算していきます。
【辺AB】
電流Iが辺ABを流れるとき、その向きは磁界の向き(磁束密度B0の向き)と同じ方向です。これでは両者が直交する成分が0のため、電磁力は発生しません。よって、辺ABに働く電磁力FABは0[N]となります。
【辺BC】
電流Iが辺BCを流れるとき、電流Iは画面下向き、磁束密度B0は画面右向きと直交しているため、フレミングの左手の法則により、画面奥から手前方向に働く電磁力FBCが発生します。
また、電磁力の大きさFは次の式で表すことができます。これは最重要公式として押さえておくべき式です。
![]()
- F:電磁力[N]
- B:磁束密度[T]
- I:電流[A]
- l:長さ[m]
よって、辺BCに働く電磁力FBCは次のように計算することができます。くり返しになりますが、向きは画面奥から手前です。
![]()
【辺CD】
電流Iが辺CDを流れるとき、その向きは磁界の向き(磁束密度B0の向き)と真逆の方向です。これも辺ABのときと同様、両者が直交する成分が0のため、電磁力は発生しません。よって、辺CDに働く電磁力FCDも0[N]となります。
【辺DA】
電流Iが辺DAを流れるときは、辺BCのときと同じように考えることができます。電流の向きが異なるのでその点を注意してフレミングの左手の法則を用いると、今度は画面手前から奥方向に電磁力が働くことがわかります。FDAの大きさは、FBCと同じです。
【上記の合計】
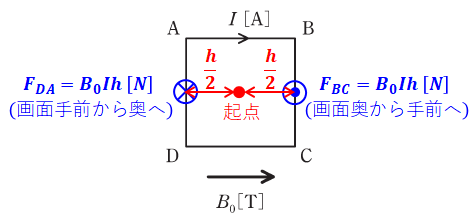
以上をまとめると、電磁力の合計は下図のようになります。
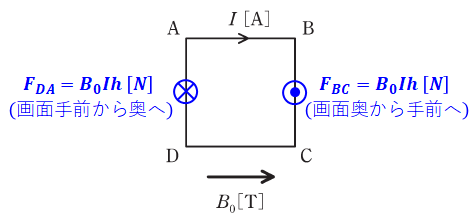
これは、正方形ABCDをくるくると回転させるような力であることがわかります。このように物体の中心が動かずに回転だけするような2つの力(向きが反対で大きさが同じ2つの力)を偶力といいます。よって、正解は(3)または(4)ということになります。
ここで、(3)や(4)を選ぶ場合には、上図に描かれた電磁力の値を使えばよいのではなく、モーメントの大きさを答えることになっているので、これを計算しなくてはなりません。
モーメントは力と距離の積で求めることができます。計算過程は色々考えられますが、どのようにやっても同じ答えになるはずなので、以下では参考までに2つの計算式によって求めてみます。本番の試験は1パターンの計算で十分です。
まずは辺DAの中心を起点として計算する方法を考えます。下図のように辺DAの中心を起点としてモーメントMを計算すると、次のようになります。
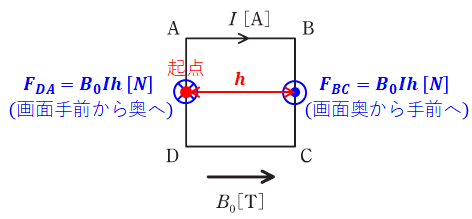
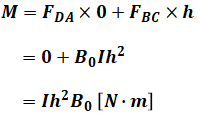
これが答えとなりますが、別のパターンとして、正方形ABCDの中心を起点として考えてみます。すると、モーメントMは次のように計算することができます。先ほどの方法と比べて、ご自分の考えやすいほうを採用してください。
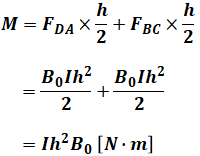
以上から、正解は(3)です。

コメント