電験三種 R2年 電力 問17 問題と解説

　問 題　　　　　

図のような系統構成の三相3線式配電線路があり、開閉器Sは開いた状態にある。各配電線のB点、C点、D点には図のとおり負荷が接続されており、各点の負荷電流はB点40A、C点30A、D点60A一定とし、各負荷の力率は100%とする。

各区間のこう長はA-B間1.5km、B-S(開閉器)間1.0km、S(開閉器)-C間0.5km、C-D間1.5km、D-A間2.0kmである。

ただし、電線1線当たりの抵抗は0.2Ω/kmとし、リアクタンスは無視するものとして、次の(a)及び(b)の問に答えよ。

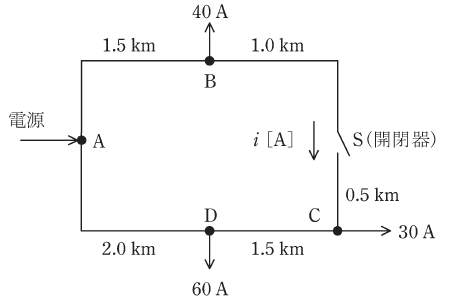
(a)　電源A点から見たC点の電圧降下の値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、電圧は相間電圧とする。

1. 41.6
2. 45.0
3. 57.2
4. 77.9
5. 90.0

(b)　開閉器Sを投入した場合、開閉器Sを流れる電流iの値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 20.0
2. 25.4
3. 27.5
4. 43.8
5. 65.4

 

 

 

 

 

　解 説　　　　

(a)

(a)では開閉器Sが開いているので、問題文の回路図のうちBC間に電流が流れることはないので、以下のように描き換えることができます。

 

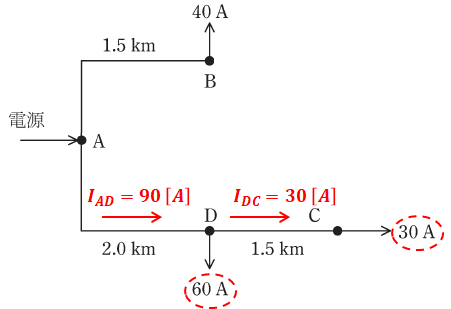
上図と問題文にある「電線1線当たりの抵抗は0.2Ω/km」という条件から、AD間の抵抗R_ADとDC間の抵抗R_DCはそれぞれ以下のようになります。

また、AD間を流れる電流I_ADは30[A]と60[A]の合計なので、90[A]となります。よって、AD間の電圧降下V_ADとDC間の電圧降下V_DCはそれぞれ次のように計算できます。

以上から、電源A点から見たC点の電圧降下V_ACは次のように求められます。

よって、正解は(4)です。

(b)

今度は開閉器Sが閉じています。下図は、問題の回路に各区間の抵抗を書き込んだものです。抵抗の求め方は(a)と同様で、0.2[Ω/km]に各区間のこう長を掛けています。また、各区間を流れる電流を下図のように設定しています。

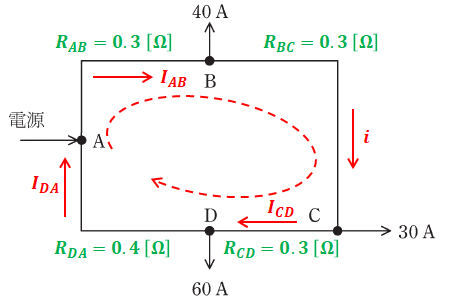
上図において、赤矢印で示した閉回路(点A→点B→点C→点D→点A)でキルヒホッフの第二法則(電圧則)を用いると、以下の等式が成り立ちます。

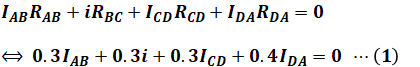
次に、キルヒホッフの第一法則(電流則)により、各区間の電流I_AB、I_CD、I_DAは次のようにiを使って表すことができます。

(2)～(4)式を(1)式に代入してiについて解けば、求める答えが得られます。

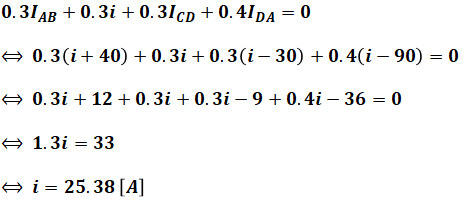
よって、正解は(2)です。