問 題
図のように線間電圧200V、周波数50Hzの対称三相交流電源にRLC負荷が接続されている。R=10Ω、電源角周波数をω[rad/s]として、ωL=10Ω、1/ωC=20Ωである。次の(a)及び(b)の問に答えよ。
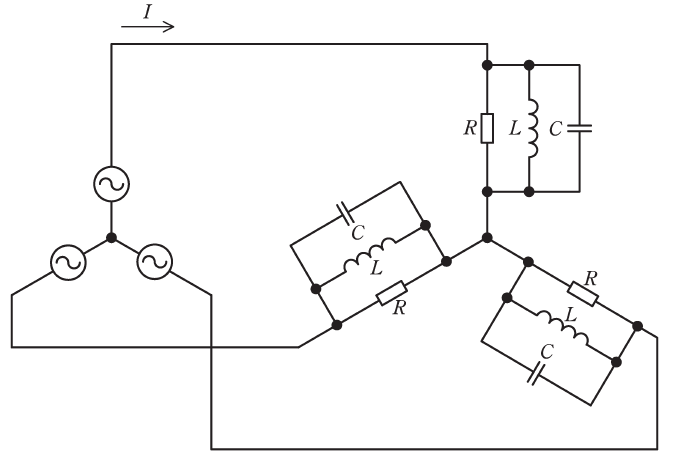
(a) 電源電流Iの値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 7
- 10
- 13
- 17
- 22
(b) 三相負荷の有効電力の値[kW]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1.3
- 2.6
- 3.6
- 4.0
- 12
解 説
(a)
問題の回路図はY‐Y結線の三相回路となっています。Y結線の中心から中性線を引いて1相あたりの等価回路を取り出すと、相電圧は線間電圧の√3分の1倍になるので、以下のような回路図を描くことができます。
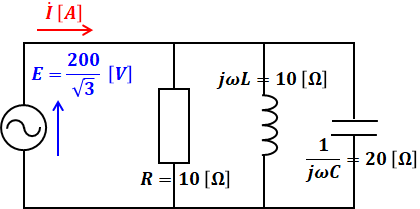
上図を見るとこの回路図はRLC並列回路であることがわかります。回路全体のインピーダンスZは、並列回路ということで、抵抗R、コイルのリアクタンスXL、コンデンサのリアクタンスXCそれぞれの逆数の和が、Zの逆数となります。
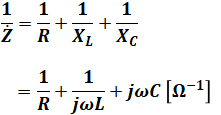
よって、これに問題文で与えられた数値を代入すると、次のようにZを計算することができます。
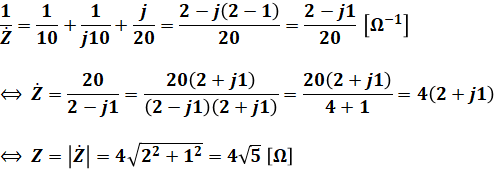
以上から、電源電流Iは次のように算出できます。
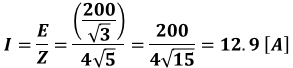
(b)
(a)で1相分の等価回路を使って考えたので、(b)でもまずは1相分の有効電力を求め、それを3倍することで三相負荷の有効電力を求めます。
(a)より電流Iは13[A]とわかっていますが、今回は有効電力が問われているので、13[A]のうち抵抗Rに流れる電流IRがどのくらいであるかを考えなくてはなりません。
とはいえ、(a)の計算過程ですでに抵抗RとリアクタンスXの比が2:1だとわかっているので、以下のような直角三角形を描いて三平方の定理を使うことにより、抵抗Rに流れる電流IRを計算することができます。
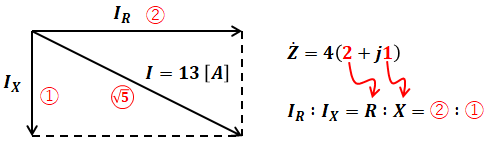
![]()
よって、1相分の有効電力PはIR2Rで求めることができるので、これを3倍したものが三相負荷の有効電力の値となります。
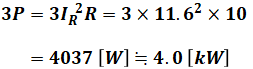

コメント