電験三種 R1年 理論 問9 問題と解説

　問 題　　　　　

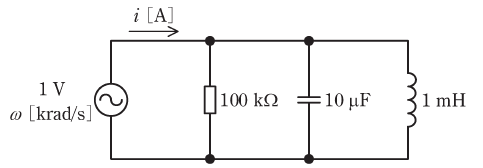
図は、実効値が1Vで、角周波数ω[krad/s]が変化する正弦波交流電源を含む回路である。

いま、ωの値がω₁=5krad/s、ω₂=10krad/s、ω₃=30krad/sと3通りの場合を考え、ω=ω_k(k=1,2,3)のときの電流i[A]の実効値をI_kと表すとき、I₁、I₂、I₃の大小関係として、正しいものを次の(1)～(5)のうちから一つ選べ。

1. I₁ ＜ I₂ ＜ I₃
2. I₁ ＝ I₂ ＜ I₃
3. I₂ ＜ I₁ ＜ I₃
4. I₂ ＜ I₁ ＝ I₃
5. I₃ ＜ I₂ ＜ I₁

 

 

 

 

 

　解 説　　　　

問題の回路図を見ると、抵抗R、コイルX_L、コンデンサX_Cが並列に並んでいることがわかります。このような回路をRLC並列回路といいます。

今回は角周波数ωが変化したときの電流の大小関係が問われていますが、RLC並列回路においては、以下の式が成り立つときに電源を流れる電流が最小になります。

これはRLC並列回路の共振の条件という重要事項です。このまま公式として覚えておきたい知識ですが、もしこの式に馴染みがない場合は、RLC並列共振回路のページを参考にしてください。

要するに、上式の左辺と右辺が一致すれば電流は最小となり、その差が大きければ大きいほど電源を流れる電流は大きくなります。

よって、次の式にω＝5、10、30[krad/s]を代入して、差(絶対値)が大きければIも大きく、差が小さければIも小さくなります。

ωにそれぞれの値を代入すると、次のようになります。

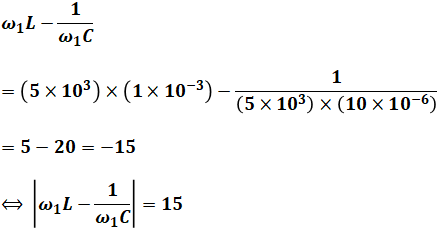
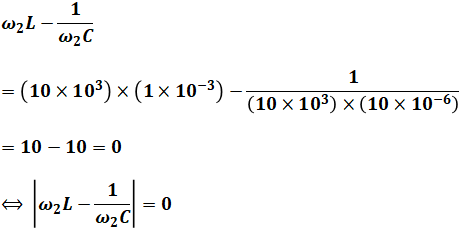
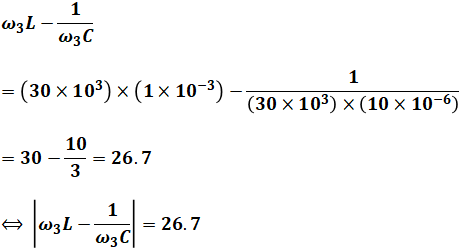
以上から、I₂ ＜ I₁ ＜ I₃ となるので、正解は(3)です。