電験三種 R1年 理論 問1 問題と解説

　問 題　　　　　

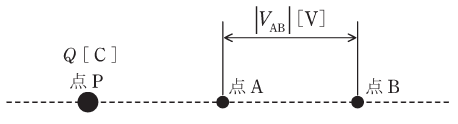
図のように、真空中に点P、点A、点Bが直線上に配置されている。点PはQ[C]の点電荷を置いた点とし、A-B間に生じる電位差の絶対値を|V_AB|[V]とする。

次の(a)～(d)の四つの実験を個別に行ったとき、|V_AB|[V]の値が最小となるものと最大となるものの実験の組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

[実験内容]

• (a) P-A間の距離を2m、A-B間の距離を1mとした。
• (b) P-A間の距離を1m、A-B間の距離を2mとした。
• (c) P-A間の距離を0.5m、A-B間の距離を1mとした。
• (d) P-A間の距離を1m、A-B間の距離を0.5mとした。

1. (a)と(b)
2. (a)と(c)
3. (a)と(d)
4. (b)と(c)
5. (c)と(d)

 

 

 

 

 

　解 説　　　　

点電荷の作る電位は以下の式で表すことができます。これは最重要事項として押さえておきたい公式です。

電位を数式化すると以下のようになります。

• V：電位 [V]
• ε₀：真空の誘電率 [F/m]
• Q：電荷 [C]
• r：点電荷からの距離 [m]

この問題で求めたいのはA-B間に生じる電位差の絶対値|V_AB|ですが、これは直接計算することができないので、上記の公式を使ってV_AとV_Bを求め、その差の絶対値をとることで|V_AB|を計算します。

たとえば条件(a)の場合のV_AとV_BをそれぞれV_A(a)、V_B(a)と表すと、これらは以下のように計算することができます。ちなみに、P-A間の距離は問題文に与えられた通りで、P-B間の距離はP-A間の距離とA-B間の距離の和です。

よって、|V_AB(a)|は次のようになります。

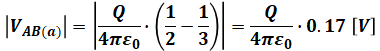
条件(b)、(c)、(d)についても同様に計算を進めると、次のようになります。

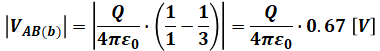
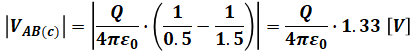
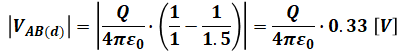
以上から、条件(a)、(b)、(c)、(d)の計算結果の共通項を除いた部分の数値は、それぞれ0.17、0.67、1.33、0.33になることがわかるので、最小は(a)、最大は(c)と判断できます。

以上から、正解は(2)です。