電験三種 R1年 機械 問8 問題と解説

　問 題　　　　　

2台の単相変圧器があり、それぞれ、巻数比(一次巻数/二次巻数)が30.1、30.0、二次側に換算した巻線抵抗及び漏れリアクタンスからなるインピーダンスが(0.013+j0.022)Ω、(0.010+j0.020)Ωである。

この2台の変圧器を並列接続し二次側を無負荷として、一次側に6600Vを加えた。

この2台の変圧器の二次巻線間を循環して流れる電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、励磁回路のアドミタンスの影響は無視するものとする。

1. 4.1
2. 11.2
3. 15.3
4. 30.6
5. 61.3

 

 

 

 

 

　解 説　　　　

問題文では巻数比と一次側の電圧の値が与えられています。巻数と電圧は比例するので、巻数比と電圧の関係は以下の式で表すことができます。

• α：巻数比
• N₁：一次側の巻数 [回]
• N₂：二次側の巻数 [回]
• E₁：一次側の誘導起電力 [V]
• E₂：二次側の誘導起電力 [V]

よって、二次側の2台の変圧器をA、Bで区別すると、それぞれの誘導起電力E_2A、E_2Bは次のように計算することができます。

以上の結果と問題文で与えられた各数値をまとめると、変圧器の二次側は以下に示すような等価回路として描くことができます。

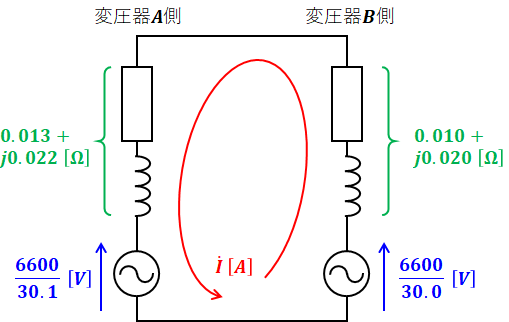
上図から、キルヒホッフの第二法則を使うと、次のように電流Iを算出できます。

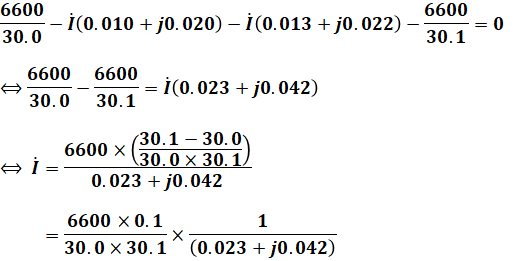
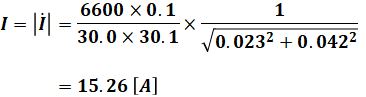
よって、正解は(3)となります。