電験三種 R1年 法規 問11 問題と解説

　問 題　　　　　

電気使用場所の低圧幹線の施設について、次の(a)及び(b)の問に答えよ。

(a)　次の表は、一つの低圧幹線によって電気を供給される電動機又はこれに類する起動電流が大きい電気機械器具(以下この問において「電動機等」という。)の定格電流の合計値I_M[A]と、他の電気使用機械器具の定格電流の合計値I_H[A]を示したものである。

また、「電気設備技術基準の解釈」に基づき、当該低圧幹線に用いる電線に必要な許容電流は、同表に示すI_Cの値[A]以上でなければならない。ただし、需要率、力率等による修正はしないものとする。

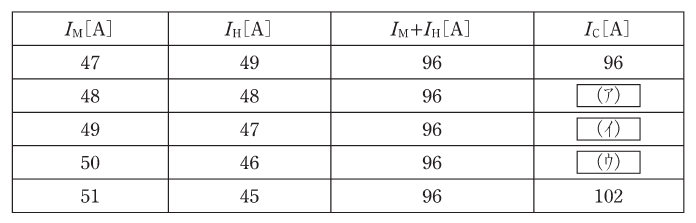
上記の表中の空白箇所(ア)、(イ)及び(ウ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

• (ア)　　(イ)　　(ウ)

1. 96　　  109　　101
2. 96　　  108　　109
3. 96　　  109　　109
4. 108　　108　　109
5. 108　　109　　101

(b)　次の表は、「電気設備技術基準の解釈」に基づき、低圧幹線に電動機等が接続される場合における電動機等の定格電流の合計値I_M[A]と、他の電気使用機械器具の定格電流の合計値I_H[A]と、これらに電気を供給する一つの低圧幹線に用いる電線の許容電流I_C’[A]と、当該低圧幹線を保護する過電流遮断器の定格電流の最大値I_B[A]を示したものである。

ただし、需要率、力率等による修正はしないものとする。

上記の表中の空白箇所(エ)、(オ)及び(カ)に当てはまる組合せとして、正しいものを次の(1)～(5)のうちから一つ選べ。

• (エ)　　(オ)　　(カ)

1. 200　　200　　220
2. 200　　220　　220
3. 200　　220　　240
4. 220　　220　　240
5. 220　　200　　240

 

 

 

 

 

　解 説　　　　

(a)

低圧幹線を施設する際の電線の許容電流は、低圧幹線の各部分ごとに、その部分を通じて供給される電気使用機械器具の定格電流の合計値以上であることが求められます。この問題の記号でいえば、I_Cは(I_M＋I_H)以上とするのが基本となります。

ただし、当該低圧幹線に接続する負荷のうち、電動機等の定格電流I_Mの合計が、他の電気使用機械器具の定格電流I_Hの合計より大きい場合は、他の電気使用機械器具の定格電流I_Hの合計に次の値を加えた値以上にする必要があります。

• 電動機等の定格電流I_Mの合計が50A以下の場合は、その定格電流I_Mの合計の1.25倍
• 電動機等の定格電流I_Mの合計が50Aを超える場合は、その定格電流I_Mの合計の1.1倍

以上を踏まえて、(ア)、(イ)、(ウ)の値について考えます。

(ア)はI_MとI_Hの値が同じで「I_M＞I_H」というわけではありません。よって、上記の「ただし～」は関係がなく、単純にI_Cは(I_M＋I_H)となります。

よって、(ア)には「96」が入ります。

(イ)と(ウ)はともに「I_M＞I_H」が成り立つので、上記の「ただし～」以降のルールを適用させます。(イ)も(ウ)もI_Mが50A以下なので、I_Mを1.25倍して計算すると、次のようになります。

(イ)：

(ウ)：

ここで注意したいのが、上記の計算結果は四捨五入ではなく繰り上げるということです。108.25を四捨五入して切り捨ててしまうと、本来は108.25A以上ないといけないのに、108Aでも構わないということになってしまいます。そうではなく、安全側で考えて109Aとするのが正しいです。

よって、(イ)の108.25と(ウ)の108.5をそれぞれ切り上げるため、両方とも「109」となります。

以上から、正解は(3)です。

(b)

(b)は低圧幹線を保護する過電流遮断器の定格電流の最大値に関する出題ですが、これはマイナーな知識が問われています。出題頻度の低さを考えると、個人的にはこの問題は捨て問題としてしまっても構わないと思います。

ただし、その場合でも(a)は重要事項かつ頻出なので、(a)の知識はきちんと身につけておくことをおすすめします。

---

低圧幹線を保護する過電流遮断器の定格電流は、当該低圧幹線の許容電流I_C‘以下のものであることが求められます。

ただし、今回の問題のように低圧幹線に電動機等が接続される場合には、次に示すような条件に合う定格電流とすることができます。

• 電動機等の定格電流I_Mの合計の3倍に、他の電気使用機械器具の定格電流I_Hの合計を加えた値以下
• 上記の値が当該低圧幹線の許容電流I_C‘を2.5倍した値を超える場合は、その許容電流I_C‘を2.5倍した値以下

以上を踏まえて、(エ)、(オ)、(カ)の値について考えます。

(エ)に関して、この場合、I_Mの3倍にI_Hを足すと次のようになります。

これはI_C‘を2.5倍した値(＝220)以下なので、上記の計算結果であるI_B＝200がそのまま(エ)の答えとなります。

(オ)に関して、この場合、I_Mの3倍にI_Hを足すと次のようになります。

これはI_C‘を2.5倍した値(＝220)以下なので、I_B＝220が(オ)の答えとなります。

ちなみに、分岐点の条件が「以下」だったか「未満」だったかで悩む必要はありません。今回のようにちょうど「3I_M＋I_H」の値と「2.5I_C‘」の値が一致するときは、どちらを使っても同じ答えが得られます。

(カ)に関して、この場合、I_Mの3倍にI_Hを足すと次のようになります。

これはI_C‘を2.5倍した値(＝220)を超えるので、I_Bは上式の計算結果ではなく、I_C‘を2.5倍した値(＝220)を用います。よって、I_B＝220が(カ)の答えとなります。

以上から正解は(2)となります。