電験三種 R1年 電力 問17 問題と解説

　問 題　　　　　

三相3線式配電線路の受電端に遅れ力率0.8の三相平衡負荷60kW(一定)が接続されている。次の(a)及び(b)の問に答えよ。

ただし、三相負荷の受電端電圧は6.6kV一定とし、配電線路のこう長は2.5km、電線1線当たりの抵抗は0.5Ω/km、リアクタンスは0.2Ω/kmとする。

なお、送電端電圧と受電端電圧の位相角は十分小さいものとして得られる近似式を用いて解答すること。また、配電線路こう長が短いことから、静電容量は無視できるものとする。

(a)　この配電線路での抵抗による電力損失の値[W]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 22
2. 54
3. 65
4. 161
5. 220

(b)　受電端の電圧降下率を2.0%以内にする場合、受電端でさらに増設できる負荷電力(最大)の値[kW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。ただし、負荷の力率(遅れ)は変わらないものとする。

1. 476
2. 536
3. 546
4. 1280
5. 1340

 

 

 

 

 

　解 説　　　　

(a)

まずは三相3線式のうち1相と中性線とを結んだ等価回路を以下に示します。

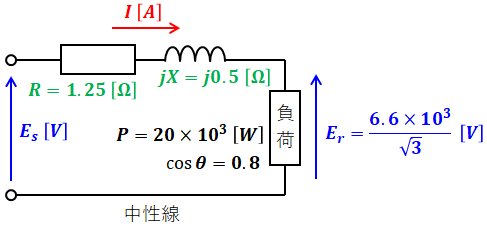
• E_s：送電端電圧 [V]
• E_r：受電端電圧 [V]
• I：線電流 [A]
• R：抵抗(電線1条あたり) [Ω]
• X：リアクタンス(電線1条あたり) [Ω]
• P：負荷での電力(1相分) [W]
• cosθ：力率

ここで、RとXの値は問題文で1kmあたりの値として与えられています。配電線路のこう長は2.5kmなので、上図には掛け算した値を記入しています。また、三相負荷が60kWなので、1相分は20kWです。

上図より、電流Iは次のように計算できます。

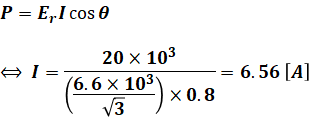
よって、1相あたりの等価回路において、配電線路での抵抗による電力損失P_lossは次のように計算できます。

上記は1線分の電力損失なので、これを3倍することで三相3線式配電線路全体の電力損失となります。

以上から、正解は(4)です。

(b)

3線式送電線における電圧降下の式は、以下のように表すことができます。これは重要公式としてそのまま覚えておきたい知識ですが、もし導出方法を知りたい場合は三相3線式送電線の電圧降下のページを参照してください。

• V_d：電圧降下 [V]
• V_s：送電端電圧 [V]
• V_r：受電端電圧 [V]
• I：線電流 [A]
• R：抵抗(電線1条あたり) [Ω]
• X：リアクタンス(電線1条あたり) [Ω]
• cosθ：負荷の力率

今回の条件ではV_dが最大でV_rの2%なので、最大のV_dは次のように計算できます。

これを上記の電圧降下の式に代入しますが、その前にcosθの値を用いてsinθの値を計算しておきます。

続いて、(2)式と(3)式を(1)に代入します。

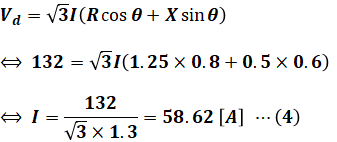
これで受電端の三相負荷を流れる電流を求めることができたので、三相負荷電力P’を算出します。

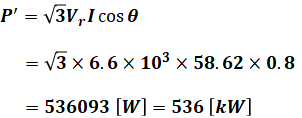
以上から、三相負荷電力は最大で536[kW]まで上げられるので、すでに設置されている60[kW]分を差し引けば、増設分を求めることができます。

よって、正解は(1)です。