電験三種 R1年 電力 問16 問題と解説

　問 題　　　　　

送電線のフェランチ現象に関する問である。三相3線式1回線送電線の一相が図のπ形等価回路で表され、送電線路のインピーダンスjX=j200Ω、アドミタンスjB=j0.800mSとし、送電端の線間電圧が66.0kVであり、受電端が無負荷のとき、次の(a)及び(b)の問に答えよ。

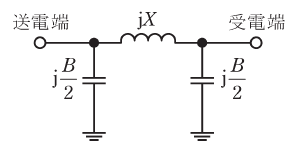
(a)　受電端の線間電圧の値[kV]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 66.0
2. 71.7
3. 78.6
4. 114
5. 132

(b)　1線当たりの送電端電流の値[A]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 15.2
2. 16.6
3. 28.7
4. 31.8
5. 55.1

 

 

 

 

 

　解 説　　　　

(a)を解く前に、まず確認しておきたいのが、アドミタンスY[S](単位：ジーメンス)とは、インピーダンスZ[Ω]の逆数です。たとえば、電流I[A]は、電圧E[V]とインピーダンスZ[Ω]から求めることができる一方、アドミタンスY[S]を使うこともできます。

そのため、アドミタンスで表すことのできる式は全てインピーダンスで表すことができますが、インピーダンスを使うと分数の計算が煩雑になりそうな場合など、アドミタンスを使ったほうが便利なこともあります。

以上を踏まえて、問題の解説を始めます。

(a)

問題文で与えられている数値を図に記入していくと、下図のような感じになります。

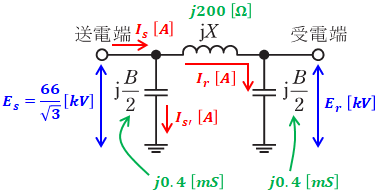
上図より、送電端と受電端の間にはインピーダンスjXがあり、そこを流れる電流をI_rとすると、送電端の相電圧E_sと受電端の相電圧E_rの間には以下の関係式が成り立ちます。

一方、受電端に注目すると、相電圧E_r、電流I_r、アドミタンスjB/2に対してオームの法則を適用させることで、次の式が成り立ちます。解説の冒頭で示した通り、アドミタンスはインピーダンスの逆数なので、電圧とアドミタンスの積が電流となります。

(1)式と(2)式のパラメータのうち、E_s、X、Bは既知の値なので、(2)式を(1)式に代入すると、相電圧E_rを計算することができます。

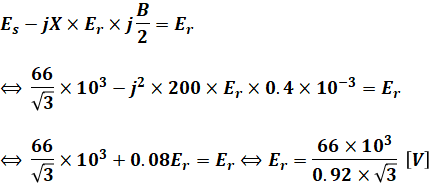
このあとの計算を踏まえて上式は計算途中で止めていますが、この段階で最後まで計算しても構いません。このあたりの処理の仕方は好みの問題ですし、どのようにやっても大した時間的ロスにはならないと思うので、あまり気にしなくて大丈夫です。

ここで、問題で与えられている図は三相3線式1回線送電線の1相分の等価回路です。上記で求めたE_rは1相分の受電端相電圧ですが、問われているのは受電端の線間電圧です。よって、E_rを√3倍したものが答えとなります。

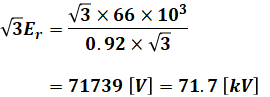
以上から、正解は(2)です。

(b)

まずは(a)の解説の冒頭に載せた図を再度示します。

上図の通り、送電端電流I_sは、受電端側のアドミタンスを流れる電流I_rと送電端側のアドミタンスを流れる電流I_s’の和となります。

ここで、I_rは(a)で計算したように電圧E_rとアドミタンスjB/2の積で表すことができ、I_s’も同様に電圧E_sとアドミタンスjB/2の積で表すことができます。

よって、以下のように計算することで、送電端電流I_sを求めることができます。

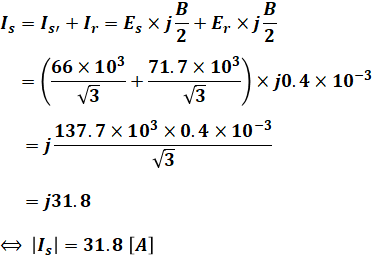
以上から、正解は(4)となります。