電験三種 R1年 電力 問15 問題と解説

　問 題　　　　　

復水器の冷却に海水を使用し、運転している汽力発電所がある。このときの復水器冷却水流量は30m³/s、復水器冷却水が持ち去る毎時熱量は3.1×10⁹kJ/h、海水の比熱容量は4.0kJ/(kg・K)、海水の密度は1.1×10³kg/m³、タービンの熱消費率は8000kJ/(kW・h)である。

この運転状態について、次の(a)及び(b)の問に答えよ。

ただし、復水器冷却水が持ち去る熱以外の損失は無視するものとする。

(a)　タービン出力の値[MW]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 350
2. 500
3. 700
4. 800
5. 1000

(b)　復水器冷却水の温度上昇の値[K]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

1. 3.3
2. 4.7
3. 5.3
4. 6.5
5. 7.9

 

 

 

 

 

　解 説　　　　

(a)

タービンに送られる蒸気のもつ熱量は、一部がタービンの出力として使われ、残りは復水器へと送られます。よって、次のような式が成り立ちます。

• Q_in：タービンに送られる蒸気の毎時熱量 [kJ/h]
• Q_out：タービン出力 [kW]
• Q‘：復水器に送られる蒸気の毎時熱量 [kJ/h]

上式のQ_outの係数が3600になっているのは、単位を揃えるためです。[W]＝[J/s]なので、Q_inやQ’と同じように1時間(60×60秒)を基準にすると、3600倍する必要があります。

この問題で問われているのはタービン出力Q_outなので、Q_inとQ’を求めて上式から計算するのが解法の流れとなります。ただし、Q’は問題文で3.1×10⁹[kJ/h]と与えられているため、あとはQ_inだけ考えればよいです。

問題文にはタービンに入る熱量に関する情報が与えられていませんが、タービンの熱消費率が8000[kJ/(kW・h)]であるとわかっています。熱消費率の単位を見てもわかるように、熱消費率とは1[kW・h]を発電するのに必要な熱量のことです。

もっと簡単にいえば、「出力に対する入力の値」ということもできます。よって、熱消費率をJ[kJ/(kW・h)]とすると、以下の等式が成り立ちます。

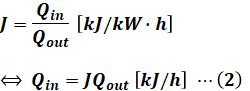
よって、(2)式を(1)式に代入し、Q_outについて解きます。

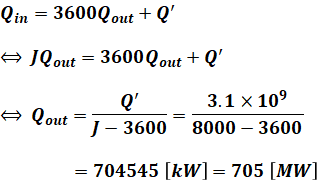
以上から、正解は(3)となります。

(b)

問題文より復水器冷却水が持ち去る毎時熱量は3.1×10⁹[kJ/h]です。この熱量に対して水の温度がどれくらい上がるかということが問われています。

今回は復水器冷却水流量が30[m³/s]なので、1時間あたりに換算すると海水量は30×3600[m³/h]となります。

また、海水の密度は1.1×10³[kg/m³]なので、上記の海水量を掛けることで体積を質量に変換できます。

さらに、海水の比熱容量は4.0[kJ/(kg・K)]と与えられています。これは、海水1[kg]の温度を1[K]上げるのに必要な熱量を指しています。

以上の3つを掛け合わせることで、海水30[m³]の温度を1[K]上げるのに必要な熱量を計算することができます。

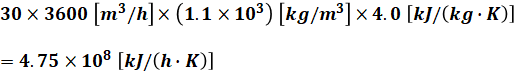
よって、3.1×10⁹[kJ/h]の熱量による海水30[m³]の温度上昇の値は、次のように計算できます。

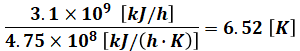
以上から、正解は(4)となります。