鳳・テブナンの定理(基礎)

電気回路の電流や抵抗を計算する際に、覚えておきたいルールがいくつかあります。たとえば、キルヒホッフの法則、重ね合わせの原理、鳳・テブナンの定理などです。この項と次の項では鳳・テブナンの定理を解説します。

鳳(ほう)・テブナンの定理は、ごちゃごちゃした(複雑な)電気回路において、ある1箇所での電流値や電圧を求める際に便利な定理です。具体的な計算方法は次項で説明しますが、鳳・テブナンの定理を用いれば、どんなに複雑な回路でも、ターゲットとしている「ある1箇所」(の抵抗など)以外の部分を、1つの抵抗と1つの電源に置き換えることができます。

ちなみに、「鳳」を付けずに単に「テブナンの定理」と呼ぶ場合もありますが、これも全く同じものです。

たとえば、以下のような電気回路があって、抵抗Rを流れる電流の大きさIが知りたいとします。

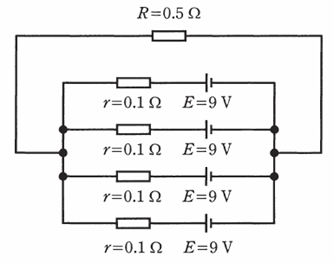
上図の電気回路は結構複雑な構成をしています。下半分にある4つの並行な抵抗rはどれも同じ抵抗値ですが、それぞれに電源があるせいで合成抵抗も簡単には求められません。

しかし、鳳・テブナンの定理を使うと、目的とする抵抗R以外の部分を1つの抵抗と1つの電源に置き換えることができるので、上図の電気回路は、以下のような等価回路に描き換えることが可能です。

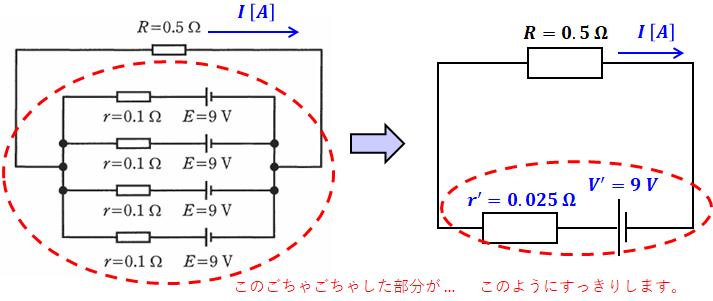
こうなれば、かなり単純な回路になったので、次のような計算によって電流Iを求めることができます。

以上が、鳳・テブナンの定理の概要です。便利な定理である一方、その計算方法をちゃんと押さえておかないと全く役に立たないので、次項で紹介する計算方法をしっかり理解して、適切なタイミングで使えるようにしておいてください。