合成抵抗

前項ではオームの法則を紹介しましたが、実際にはこの公式1つで問題が解けることはほとんどありません。オームの法則に加え、抵抗の合成や各種の定理なども覚えておかなくてはいけないので、この項以降では、それらについて1つずつ解説していきます。

まず、本項では抵抗の合成について紹介します。

合成抵抗

回路に抵抗が2つ以上ある場合、そのままでは計算がしづらいので、複数の抵抗を1つにまとめる操作が必要です。まずは以下のように2つの抵抗が直列に並んでいる場合、その抵抗は単純に足し合わせることができます。

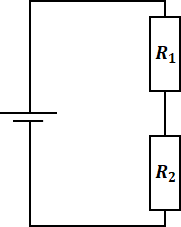
一方、2つの抵抗が並列に並んでいる場合、合成抵抗の逆数がそれぞれの抵抗の逆数の和になります。

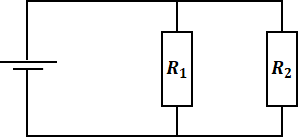
上式の右辺を通分してから、両辺の分母と分子をひっくり返すと、次のようになります。

直列と並列、それぞれの合成抵抗の式を覚えておけば、あとは組み合わせの問題になります。たとえば、以下の回路の合成抵抗は次の通りです。

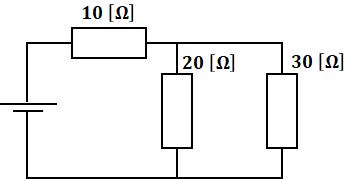
まずは20[Ω]と30[Ω]の合成です。これは並列に並んでいるので、分数の式のほうを使います。

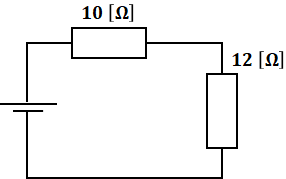
続いて、10[Ω]と12[Ω]の合成です。これは直列に並んでいるので、そのまま足します。

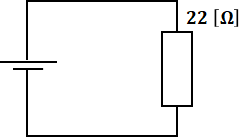
よって、3つの抵抗の合成抵抗は22[Ω]ということになります。