問 題
次の文章は、磁界中の電子の運動に関する記述である。
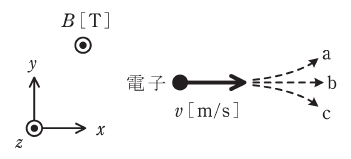
図のように、平等磁界の存在する真空かつ無重力の空間に、電子をx方向に初速度v[m/s]で放出する。平等磁界はz方向であり磁束密度の大きさB[T]をもつとし、電子の質量をm[kg]、素電荷の大きさをe[C]とする。
ただし、紙面の裏側から表側への向きをz方向の正とし、vは光速に比べて十分小さいとする。
このとき、電子の運動は( ア )となり、時間T=( イ )[s]後に元の位置に戻ってくる。電子の放出直後の軌跡は破線矢印の( ウ )のようになる。
一方、電子を磁界と平行なz方向に放出すると、電子の運動は( エ )となる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。

解 説
問題文の冒頭で「磁界中の電子の運動」と書いてある時点で、等速円運動を思い浮かべてほしいです。なので、試験本番でこのような出題があれば、( ア )は計算式を使うまでもなく「等速円運動」だと判断したいところです。
…とはいえ、それだと何の解説にもなっていないので、以下にきちんと計算式を使った導出を行います。
問題文によると、磁束密度B[T]の一様な磁界が画面の奥から手前へ垂直に加わっています。この向きは◯の中に●がある記号から判断できます。もし◯の中に×が描かれていたら、画面の手前から奥への向きを表します。
ここで、電荷e[C]、質量m[kg]の電子を置き、x方向に速さv[m/s]の初速度を与えると、この電子は初速度の向きとも磁界の向きとも垂直になる方向の電磁力F[N]を受けます。磁界の中を運動する電子が受けるこの電磁力F[N]のことを、ローレンツ力といい、以下の式で表されます。
![]()
- F:ローレンツ力[N]
- B:磁束密度[T]
- e:電子の電荷[C]
- v:電子の速度[m/s]
電子が受けるローレンツ力の向きが電子の速度の向きと垂直ということは、この電子は加速も減速もせず、ただ向きだけが変わります。するとカーブするように動きますが、曲がりながらもその都度その進行方向に対して垂直向きに力を受け続けるので、結果として、この電子は速度v[m/s]のまま等速円運動をすることになります。
以上から、( ア )には「等速円運動」が入ります。
( イ )は周期Tが問われていますが、そのためには周知Tや角周波数ωを用いる以下の3つの公式を押さえておく必要があります。
Tを求めるためには、まず以下の基本的な(かつ重要な)3つの式を押さえておく必要があります。
![]()
- T:周期[s]
- f:周波数[Hz]
![]()
- ω:角周波数[rad/s]
![]()
- v:速度[m/s]
- r:半径[m]
一方、円運動の円の半径をr[m]とすると、電子に働くローレンツ力と遠心力とがつり合っていることから、以下の等式が成り立ちます。下式の左辺がローレンツ力、右辺が遠心力表しています。
![]()
これをrについて解くと、次式のようになります。
![]()
(1)式~(4)式を合わせることで、以下のように計算すれば( イ )の答えを得ることができます。
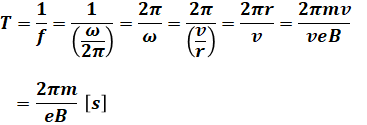
( ウ )についてはフレミングの左手の法則から考えるとよいです。ただし、フレミングの左手の法則は電流、磁界、電磁力の3つのパラメータである点に注意してください。電子の速度の向きは電流なので、そこを見落とすと正解を誤ってしまいます。
- 中指 :電流の向き(電子の速度の反対向き)
- 人差し指:磁界の向き
- 親指 :電磁力(ローレンツ力)の向き
というわけで、電子が画面右側に進むので中指(電流)は画面左側に向け、人差し指(磁界)は画面手前側に向けます。すると、親指(ローレンツ力)は画面上方向を向くため、( ウ )は「a」であることがわかります。
最後の( エ )について、今までの話は全て磁界の向きと電子の初速度の向きが垂直になっていることが前提でした。これら2つの向きのなす角が0だと、垂直成分が全くないということなので、ローレンツ力は発生しません。
よって、初速度vで進む電子は何の力も受けずにそのまま進行方向に進むだけなので、( エ )には「等速直線運動」が入ります。
以上から、正解は(5)です。

コメント
説明がわかりやすく、その都度公式も出てくるので助かります。