問 題
次の文章は、平行板コンデンサの電界に関する記述である。
極板間距離d0[m]の平行板空気コンデンサの極板間電圧を一定とする。
極板と同形同面積の固体誘電体(比誘電率εr>1、厚さd1[m]<d0[m])を極板と平行に挿入すると、空気ギャップの電界の強さは、固体誘電体を挿入する前の値と比べて( ア )。
また、極板と同形同面積の導体(厚さd2[m]<d0[m])を極板と平行に挿入すると、空気ギャップの電界の強さは、導体を挿入する前の値と比べて( イ )。
ただし、コンデンサの端効果は無視できるものとする。
上記の記述中の空白箇所(ア)及び(イ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ)
- 強くなる 強くなる
- 強くなる 弱くなる
- 弱くなる 強くなる
- 弱くなる 弱くなる
- 変わらない 変わらない
解 説
この問題は前半の( ア )がやや難しい一方、後半の( イ )はかなり基礎的な内容です。なので、少なくとも( イ )を正解して選択肢(1)と(3)の2択まで絞りたいところです。
…というわけで、ここでは( イ )のほうを先に解説します。
導体は電気が流れやすく、コイルやコンデンサのように電気を溜めておくことができません。よって、平行板コンデンサの空間部分の一部に導体を挿入するということは、単純にコンデンサの極板間の距離が狭くなるということです。
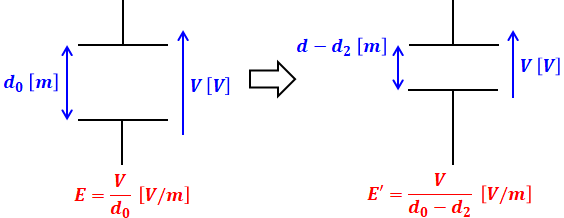
- E:電界の強さ [V/m]
- V:電圧 [V]
- d:板間距離 [m]
上図の通り、コンデンサの一部が導体に変わったところで、電気回路のほかの部分を変更していなければコンデンサの極板間電圧Vは一定です。つまり、dが小さくなれば、その分Eが大きくなるはずです。
ここで示した電界の強さEを求める式は最重要公式として押さえておく必要があります。
よって、( イ )には「強くなる」を入れるのが適切です。
続いて、( ア )の解説に入ります。
コンデンサに誘電体を挿入するというのは、図示すると次のようになります。
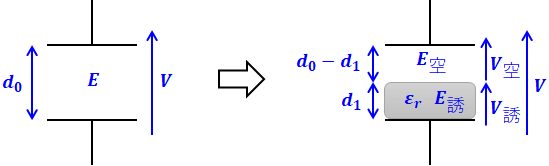
上図の左側において、( イ )のところで紹介したように、電圧Vと電界E、板間距離dの関係は次の式で表すことができます。
![]()
- V:電圧 [V]
- E:電界の強さ [V/m]
- d0:板間距離 [m]
一方、上図の右側についても誘電体部分と空気ギャップ部分の合計の電圧はVのままなので、以下のような等式が成り立ちます。
![]()
- E空:空気ギャップ部分の電界の強さ [V/m]
- E誘:誘電体部分の電界の強さ [V/m]
ここで、E空とE誘は以下の式で表すことができ、誘電体の有無に関わらず電束密度Dは不変なので、2つの式を結ぶことができます。
![]()
![]()
- D:電束密度 [C/m2]
- ε0:真空の誘電率 [F/m]
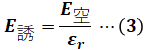
よって、(3)式を(2)式に代入すると、次のようになります。
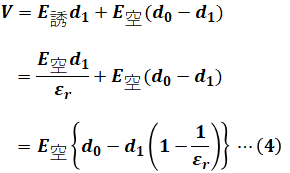
ここで、(1)式と(4)式とを組み合わせると、
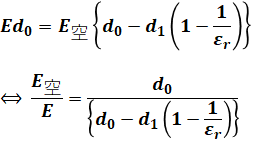
のようになります。
問題文より、εr>1、d1<d0なので、上式のE空/Eは1より大きくなることがわかります。つまり、誘電体を挿入することによって空気ギャップの電界の強さは大きくなっています。
以上から、( ア )には「強くなる」が入るため、正解は(1)となります。

コメント