問 題
定格容量P[kV・A]、定格電圧V[V]の星形結線の三相同期発電機がある。電機子電流が定格電流の40%、負荷力率が遅れ86.6%(cos30°=0.866)、定格電圧でこの発電機を運転している。
このときのベクトル図を描いて、負荷角δの値[°]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
ただし、この発電機の電機子巻線の1相当たりの同期リアクタンスは単位法で0.915p.u.、1相当たりの抵抗は無視できるものとし、同期リアクタンスは磁気飽和等に影響されず一定であるとする。
- 0
- 15
- 30
- 45
- 60
解 説
最初にp.u.という単位(厳密には単位ではありませんが…)について確認しておきます。これは、「per unit」の略です。「per」のほうは、毎秒何メートル(m/s)の「毎」のことです。「unit」は基準のことで、特に定格電圧や定格電流といった定格値を基準にすることが多いです。
つまり「p.u.」は「定格あたりの」といったような意味になります。今回の問題では同期リアクタンスが0.915p.u.なので、定格電圧を1、定格電流も1としたときの同期リアクタンスが0.915であるということです。
以上を踏まえて問題文を読み解いていきます。
まず、三相同期発電機の1相分の等価回路は次のように描くことができます。
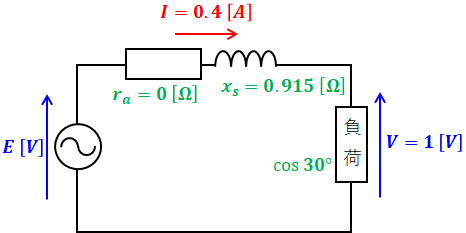
上図において、各種の数値は全部p.u.に合わせて書き込んでいます。また、E[V]は1相あたりの誘導起電力です。
以上から、ベクトル図を描くと以下のようになります。
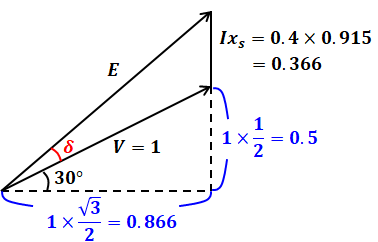
このベクトル図からわかる通り、ベクトルEの横軸の長さも縦軸の長さも、ともに0.866となります。よって、ベクトルEを斜辺とする二等辺三角形の鋭角は45°になるので、求める負荷角δは、
![]()
のように計算することができます。
よって、正解は(2)です。

コメント