電験三種 H29年 理論 問16 問題と解説

　問 題　　　　　

図のように、線間電圧V[V]、周波数f[Hz]の対称三相交流電源に、R[Ω]の抵抗とインダクタンスL[H]のコイルからなる三相平衡負荷を接続した交流回路がある。この回路には、スイッチSを介して、負荷に静電容量C[F]の三相平衡コンデンサを接続することができる。次の(a)及び(b)の問に答えよ。

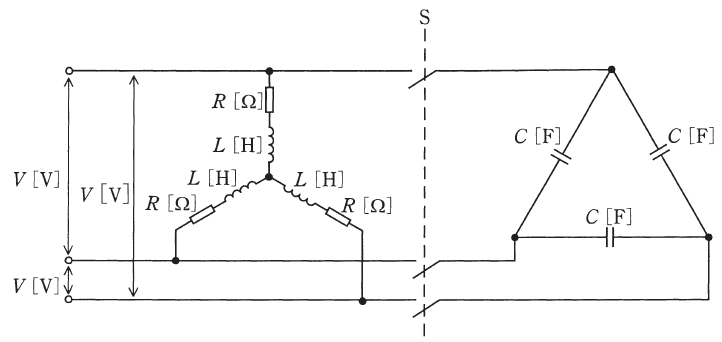
(a)　スイッチSを開いた状態において、V=200V、f=50Hz、R=5Ω、L=5mHのとき、三相負荷全体の有効電力の値[W]と力率の値の組合せとして、最も近いものを次の(1)～(5)のうちから一つ選べ。

　　有効電力　　　力率

1. 2.29×10³0.50
2. 7.28×10³0.71
3. 7.28×10³0.95
4. 2.18×10⁴0.71
5. 2.18×10⁴0.95

(b)　スイッチSを閉じてコンデンサを接続したとき、電源からみた負荷側の力率が1になった。このとき、静電容量Cの値[F]を示す式として、正しいものを次の(1)～(5)のうちから一つ選べ。ただし、角周波数をω[rad/s]とする。

 

 

 

 

 

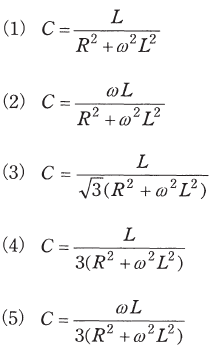
　解 説　　　　

(a)

(a)ではスイッチSを開いているので、右側のΔ結線のほうは考えません。

問題の図の三相回路ですが、これを1相あたりの等価回路に描き直すと、以下のような回路が描けます。

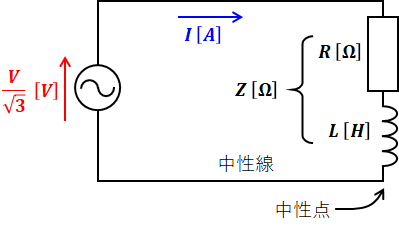
ちなみに、三相回路の線間電圧に対し、等価回路の電圧(相電圧)はその√3分の1になります。

また、コイルのリアクタンスXは、次の計算によって求められるので、RとXを合成したインピーダンスZは、以下のようになります。

この段階で、有効電力の前に力率cosθを計算することができます。その理由は、力率とは皮相電力に対する有効電力の割合のことですが、これは、インピーダンスZに対する抵抗Rの割合が全く一緒だからです。

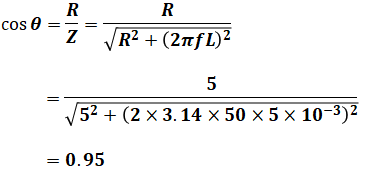
続いて、有効電力P=I²Rなので、まずは上記の等価回路を流れる電流Iを計算します。

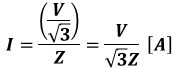
よって、この等価回路の有効電力Pは以下のようになります。

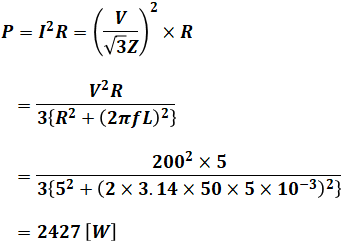
ここで求めたPは1相あたりの等価回路の有効電力です。問われているのは三相回路の有効電力なので、これを3倍しなければなりません。

以上から、(a)の正解は(3)とわかります。

(b)

抵抗とコイル側はY結線、コンデンサ側はΔ結線と異なっています。このままでは考えづらいので、こういう場合はΔ結線をY結線に変換して、どちらもY結線にして統一すると計算しやすくなります(Δ結線に統一するやり方もありますが、Δ結線は中性点が存在せず1相あたりの等価回路が描きづらいので、おすすめしません)。

Δ結線の負荷をY結線へと変換した場合、変換後のインピーダンスZ_Yは変換前のインピーダンスZ_Δの3分の1倍になります(！重要事項！)。

よって、問題の回路図から1相あたりの等価回路を描いた場合、次のようになります。

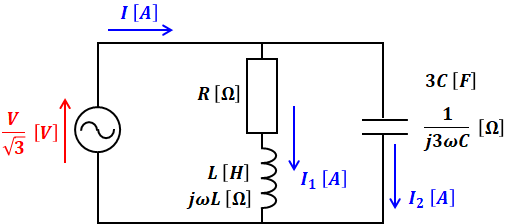
上図において、電源を流れる電流をI、抵抗とコイル側を流れる電流をI₁、コンデンサ側を流れる電流をI₂とすると、Iは以下のように表すことができます。

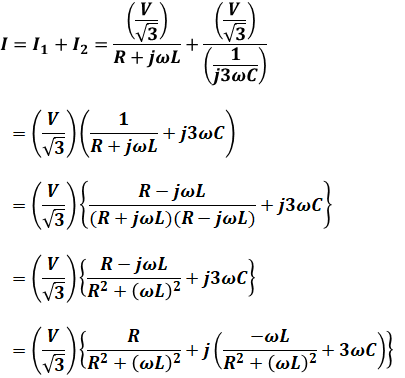
ここで、電源からみた負荷側の力率が1なので、電源を流れる電流は実数部のみで、虚数部の項は係数が0になるはずです。

よって、

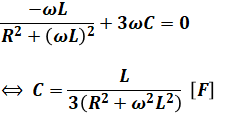
と計算することで、求めるCを導出することができます。