問 題
R1=20Ω、R2=30Ωの抵抗、インダクタンスL1=20mH、L2=40mHのコイル及び静電容量C1=400μF、C2=600μFのコンデンサからなる図のような直並列回路がある。
直流電圧E=100Vを加えたとき、定常状態においてL1、L2、C1及びC2に蓄えられるエネルギーの総和の値[J]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 0.12
- 1.20
- 1.32
- 1.40
- 1.52
正解 (5)
解 説
コイルとコンデンサに蓄えられるエネルギーが問われているので、まずはそれぞれのエネルギーを表す式を確認しておいてください。
![]()
- WL:コイルに蓄えられるエネルギー[J]
- L:コイルのインダクタンス[H]
- I:電流[A]
![]()
- WC:コンデンサに蓄えられるエネルギー[J]
- C:コンデンサの静電容量[F]
- V:電圧[V]
上記に加え、もうひとつ重要事項があります。直流回路においては(!注意!電源が直流電源のときだけ!)、定常状態だとコイルの両端の電位差は0になります。つまり、コイルの部分は「短絡」したただの導線とみなすことができます。
一方、同条件のコンデンサには電流が流れません。つまり、コンデンサの部分は「開放」している状態であるといえます。
コイルは短絡し、コンデンサは開放していると考えると、問題の回路図は以下のように描き換えることができます。
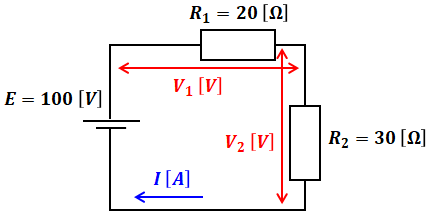
上図においてオームの法則を適用すると、この回路を流れる電流Iを求めることができます。
![]()
また、それぞれの抵抗の両端の電位差V1、V2も計算することができます。
![]()
![]()
以上で求めた数値を問題の図に書き加えると、以下のようになります。
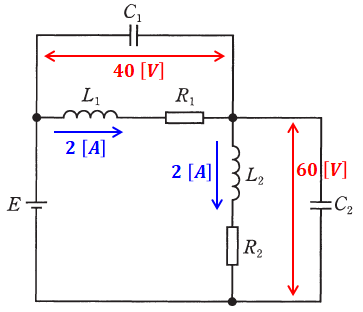
よって、L1、L2、C1、C2に蓄えられるエネルギーの総和Wは、次のように計算することができます。
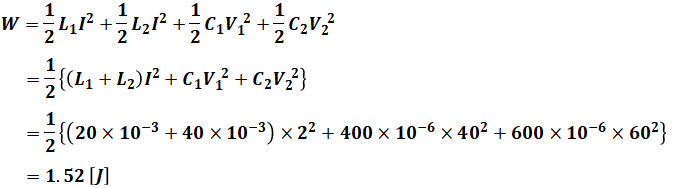
以上から、正解は(5)となります。

コメント