問 題
環状鉄心に、コイル1及びコイル2が巻かれている。二つのコイルを図1のように接続したとき、端子A-B間の合成インダクタンスの値は1.2Hであった。次に、図2のように接続したとき、端子C-D間の合成インダクタンスの値は2.0Hであった。
このことから、コイル1の自己インダクタンスLの値[H]、コイル1及びコイル2の相互インダクタンスMの値[H]の組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
ただし、コイル1及びコイル2の自己インダクタンスはともにL[H]、その巻数をNとし、また、鉄心は等断面、等質であるとする。
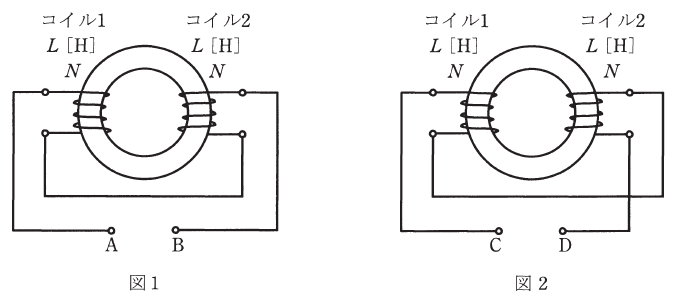
自己インダクタンスL 相互インダクタンスM
- 0.4 0.2
- 0.8 0.2
- 0.8 0.4
- 1.6 0.2
- 1.6 0.4
解 説
図1と図2の違いは電流の流れる向きですが、それによって双方のコイルに生じる磁束の向きが変わってきます。
図1の場合、仮に電流がAからBへ流れると考えた場合、右ねじの法則を使うとコイル1とコイル2にできる磁束の向きは下図のようになります。
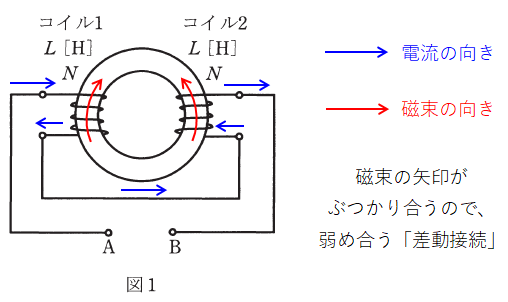
すると、コイル1にできる時計回りの磁束と、コイル2にできる反時計回りの磁束とがぶつかり合います。このような接続の仕方を「差動接続」といいます。
一方、図2の場合には、電流がCからDへ流れると考えた場合、コイル1とコイル2にできる磁束の向きは下図のように先程とは反対になります。
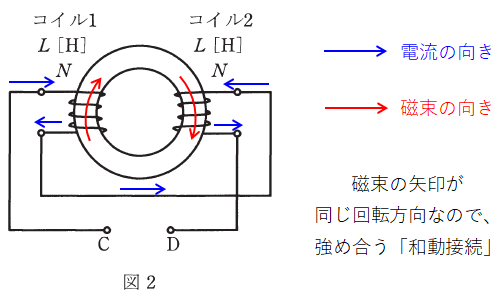
すると、コイル1とコイル2で生じる磁束の回転方向が一緒になります。このような接続の仕方を「和動接続」といいます。
合成インダクタンスは自己インダクタンスと相互インダクタンスを合成したものですが、和動接続か差動接続かによって、合成インダクタンスを表す式は以下のように異なってきます。
![]()
![]()
- Lwa:和動接続での合成インダクタンス[H]
- Lsa:差動接続での合成インダクタンス[H]
- L1:コイル1の自己インダクタンス[H]
- L2:コイル2の自己インダクタンス[H]
- M:相互インダクタンス[H]
今回の問題では、L1とL2はともに同じ値Lであり、LwaやLsaは問題文で与えられているため、上記の2つの連立方程式を解けば、LとMを求めることができます。
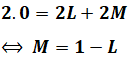
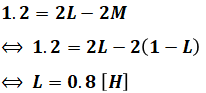
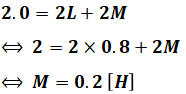

コメント