電験三種 H29年 理論 問2 問題と解説

　問題　　　　　

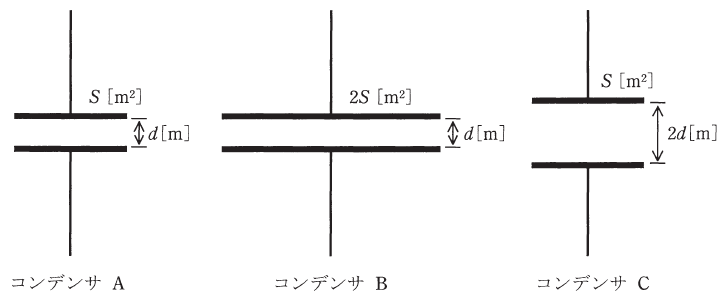
極板の面積S[m²]、極板間の距離d[m]の平行板コンデンサA、極板の面積2S[m²]、極板間の距離d[m]の平行板コンデンサB及び極板の面積S[m²]、極板間の距離2d[m]の平行板コンデンサCがある。各コンデンサは、極板間の電界の強さが同じ値となるようにそれぞれ直流電源で充電されている。

各コンデンサをそれぞれの直流電源から切り離した後、全コンデンサを同じ極性で並列に接続し、十分時間が経ったとき、各コンデンサに蓄えられる静電エネルギーの総和の値[J]は、並列に接続する前の総和の値[J]の何倍になるか。その倍率として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、各コンデンサの極板間の誘電率は同一であり、端効果は無視できるものとする。

正解 (2)

　解説　　　　

この問題では静電エネルギーの倍率が問われているので、まず、コンデンサに蓄えられるエネルギーの式を知っておく必要があります。

ここで、上式を使って静電エネルギーWを求めようとしても、静電容量Cも電圧Vも問題文では与えられていないパラメータです。そのため、既知の面積Sや距離dを使って、CやVを計算する必要があります。

静電容量Cは、以下の式で求めることができます。

電圧Vは、以下の式で求めることができます。

上式は3つとも最重要公式として押さえておいてください。

以上が前置きで、ここからが具体的な解法となります。

まず、コンデンサA、B、Cの静電容量をそれぞれC_A、C_B、C_Cとすると、上記で示した通り静電容量Cは面積Sに比例し、距離dに反比例するため、C_Aを基準とすると、C_Bはその2倍(面積が2Sなので)、C_Cはその1/2倍(距離が2dなので)となります。

一方、コンデンサA、B、Cの電圧をそれぞれV_A、V_B、V_Cとすると、電界の強さEは問題文よりどれも同じ値なので、dの違いがそのままVの違いになります。よって、ここでも基準をV_Aとすると、V_BやV_Cは次のようになります。

以上から、問題文の前半時点での静電エネルギーの和W_beforeは、次のように表すことができます。

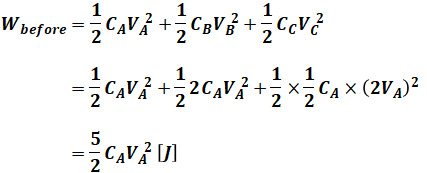
続いて問題文の後半に入ります。

3つのコンデンサを並列に接続すると、全てのコンデンサの電圧が同じ値となりますが、これは並列接続前のV_A、V_B、V_Cのどれでもない値となるため、よくわかりません。しかし、並列接続の前後において、それぞれのコンデンサに蓄えられていた電荷Qの総量に変化はありません。

よって、並列前の各コンデンサに蓄えられていた電荷をQ_A、Q_B、Q_Cとすると、Q_A+Q_B+Q_Cは常に不変です。ここで、電荷Qは静電容量Cと電圧Vを使って

と表すことができるので、並列接続前のCやVを使えば、電荷Qの総量を計算することができます。

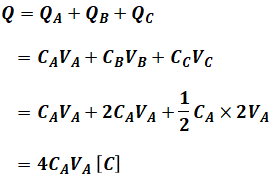
一方、並列接続前後でコンデンサの静電容量Cが変わることはないため、静電容量の合計値Cは、今まで求めた値を使って次のように計算できます。

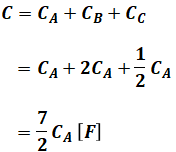
以上から、並列接続後の静電エネルギーは

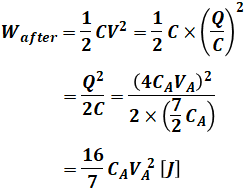
となるので、並列接続前後の静電エネルギーの比は、

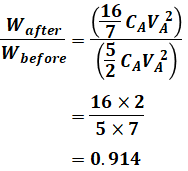
と計算することができます。

電験三種 H29年理論問2 問題と解説