問 題
定格出力15kW、定格電圧400V、定格周波数60Hz、極数4の三相誘導電動機がある。この誘導電動機が定格電圧、定格周波数で運転されているとき、次の(a)及び(b)の問に答えよ。
(a) 軸出力が15kW、効率と力率がそれぞれ90%で運転されているときの一次電流の値[A]として、最も近いものを次の(1)~(5)のうちから一つ選べ。
- 22
- 24
- 27
- 33
- 46
(b) この誘導電動機が巻線形であり、全負荷時の回転速度が1746min-1であるものとする。二次回路の各相に抵抗を追加して挿入したところ、全負荷時の回転速度が1455min-1となった。ただし、負荷トルクは回転速度によらず一定とする。
挿入した抵抗の値は元の二次回路の抵抗の値の何倍であるか。最も近いものを次の(1)~(5)のうちから一つ選べ。
- 1.2
- 2.2
- 5.4
- 6.4
- 7.4
解 説
(a)
出力Pは入力に効率ηを掛けたものとなるため、以下のような式になります。
![]()
- P:出力[W]
- V:電圧[V]
- I:電流[A]
- cosθ:力率
- η:効率
よって、上式に問題文で与えられた数値を代入してIについて解けば、電流値を求めることができます。
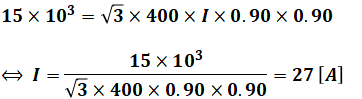
(b)
(b)のポイントは、誘導電動機が巻線形であるということと、トルクが一定であるということ、その上で抵抗値が問われているという点です。
巻線形誘導電動機のトルクTは、二次回路の巻線抵抗rと滑りsの比に関係する値をとるので、Tが一定であるならば、常にr/sの比は一定の値をとります。つまり、もとの二次巻線抵抗をr、滑りをsとし、追加した抵抗をr’、抵抗追加後の滑りをsとすると、次の等式が成り立ちます。
![]()
このように、一定のトルクを生じるための二次巻線抵抗rと滑りsとの間には比例関係があり、このような特性を比例推移といいます。
最終的に求めたいのはr’/rなので、上式を以下のように式変形します。
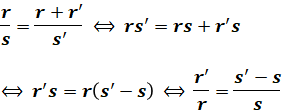
上式の右辺に具体的な数値を代入すれば答えが求められるので、このあとは滑りs、s’を計算していきます。
誘導電動機の滑りsは以下の式で表されます。これは重要公式として覚えておく必要があります。
![]()
- s:滑り
- Ns:同期速度[min-1]
- N:回転速度[min-1]
また、同期速度Nsは次の式の通りです。これも重要公式です。
![]()
- p:磁極の数[極]
- f:周波数[Hz]
以上の式に問題文で与えられた条件を代入していくと、s、s’は次のように計算することができます。
![]()
![]()
![]()
ここで求めたs、s’を先ほどの式に代入すると、問われている抵抗の比を求めることができます。
![]()

コメント