問 題
次の文章は、送風機など電動機の負荷の定常特性に関する記述である。
電動機の負荷となる機器では、損失などを無視し、電動機の回転数と機器において制御対象となる速度が比例するとすると、速度に対するトルクの代表的な特性が以下に示すように二つある。
一つは、エレベータなどの鉛直方向の移動体で速度に対して( ア )トルク、もう一つは、空気や水などの流体の搬送で速度に対して( イ )トルクとなる特性である。
後者の流量制御の代表的な例は送風機であり、通常はダンパなどを設けて圧損を変化させて流量を制御するのに対し、ダンパなどを設けずに電動機で速度制御することでも流量制御が可能である。
このとき、風量は速度に対して( ウ )して変化し、電動機に必要な電力は速度に対して( エ )して変化する特性が得られる。したがって、必要流量に絞って運転する機会の多いシステムでは、電動機で速度制御することで大きな省エネルギー効果が得られる。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ)
- 比例する 2乗に比例する 比例 3乗に比例
- 比例する 一定の 比例 2乗に比例
- 比例する 一定の 2乗に比例 2乗に比例
- 一定の 2乗に比例する 比例 3乗に比例
- 一定の 2乗に比例する 2乗に比例 2乗に比例
解 説
( ア )に関して、エレベータは電力を位置エネルギーに変換するものです。よって、エレベータの電動機の出力Pは以下の式で表すことができます。
![]()
- P:電動機の出力[W]
- M:質量[kg]
- g:重力加速度
- v:速度(1秒間の間に上昇する高さ)
一方、トルクTと角速度ωの積が出力Pなので、
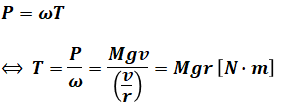
- r:滑車の半径[m]
となり、Pはvによらず一定の値を取るため、( ア )は「一定の」となります。
( イ )のほうは水の搬送(揚水)で考えると、こちらも電動機の出力Pは位置エネルギーの増加分と等しいので、以下の式で表すことができます。
![]()
- P:電動機の出力[W]
- Q:1秒あたりのポンプの流量[kg/s]
- g:重力加速度
- H:揚水した高さ
ここで、Qの水量は水の速度に比例します(1秒あたりの水量=断面積×水の速度)。また、揚水した高さは水の速度の2乗に比例します。これは、位置エネルギーと運動エネルギーの等式から以下のように考えればわかります。
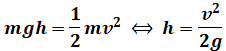
よって、電動機の出力Pは速度vの3乗に比例します(比例係数をkとすれば、P=kv3と表されます)。あとは( ア )のときと同様、トルクの式を以下のように式変形すると、
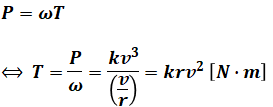
となるので、( イ )には「2乗に比例する」が入ります。
( ウ )と( エ )に関して、エレベータのような固体を動かすのと水のような流体を動かすのでは( ア )と( イ )で求めたように話が異なるのですが、問題文にもあるように、空気(気体)と水(液体)であれば、どちらも同じ流体として、同じように振る舞います。
よって、( ウ )や( エ )で問われている風の話は、上記で求めた水での考え方をそのまま用いることができます。つまり、風量は速度に比例し、電力は速度の3乗に比例するため、( ウ )には「比例」が、( エ )には「3乗に比例」が入ります。
以上から、正解は(4)であるとわかります。

コメント