問 題
電荷q[C]をもつ荷電粒子が磁束密度B[T]の中を速度v[m/s]で運動するとき受ける電磁力はローレンツ力と呼ばれ、次のように導出できる。
まず、荷電粒子を微小な長さΔl[m]をもつ線分とみなせると仮定すれば、単位長さ当たりの電荷(線電荷密度という。)は ![]() となる。
となる。
次に、この線分が長さ方向に速度vで動くとき、線分には電流![]() が流れていると考えられる。
が流れていると考えられる。
そして、この微小な線電流が受ける電磁力はF=BIΔlsinθであるから、ローレンツ力の式F=( ア )[N]が得られる。ただし、θはvとBとの方向がなす角である。FはvとBの両方に直交し、Fの向きはフレミングの( イ )の法則に従う。
では、真空中でローレンツ力を受ける電子の運動はどうなるだろうか。
鉛直下向きの平等な磁束密度Bが存在する空間に、負の電荷をもつ電子を速度vで水平方向に放つと、電子はその進行方向を前方とすれば( ウ )のローレンツ力を受けて( エ )をする。
ただし、重力の影響は無視できるものとする。
上記の記述中の空白箇所(ア)、(イ)、(ウ)及び(エ)に当てはまる組合せとして、正しいものを次の(1)~(5)のうちから一つ選べ。
(ア) (イ) (ウ) (エ)
- qvBsinθ 右手 右方向 放物線運動
- qvBsinθ 左手 右方向 円運動
- qvBΔlsinθ 右手 左方向 放物線運動
- qvBΔlsinθ 左手 左方向 円運動
- qvBΔlsinθ 左手 右方向 ブラウン運動
解 説
( ア )については、問題文に電流Iの式と電磁力Fの式が与えられているので、これを組み合わせれば答えが出せます。
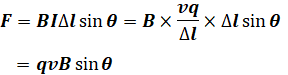
( イ )で、電磁力と電流と磁界といえば、「フレミングの左手の法則」が適用できます。これは、左手の親指と人差し指と中指を互いに直交させたとき、中指が電流の向き、人差し指が磁界の向き、親指が電磁力の向きに相当するという法則です。
ちなみに、問題文の文中では電流ではなく電荷の速度vとして扱っていますが、電荷が移動する=電流が流れる、ということなので、同じ意味合いを持ちます。
ただし、正電荷であれば電流と同方向で一致しますが、負電荷(電子)の流れる方向と電流の流れる方向は反対なので、その点は注意してください。電子の流れる方向は、中指が指す方向の真逆になります。
( ウ )について、問題文の条件を図で表すと以下のように描くことができます。
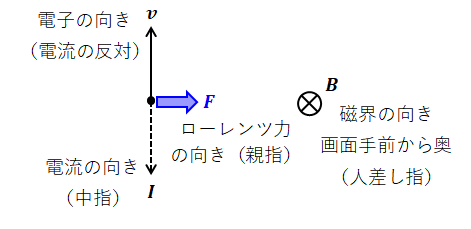
どのような描き方でも構いませんが、ここでは、最初に磁束密度Bを画面手前から奥に向けて突き通すように描きました。次に、Bの左側でに電子が下から上へと移動しているように描きます(上記の通り、電流の向きはその真逆になります)。そして、左手を出して電流の向きに中指を、磁界の向きに人差し指を合わせると、力の向きは右向きとなることがわかります。
この問題では電子の進行方向(ここでは画面上方向)が前方なので、ローレンツ力は「右方向」に働くことがわかります。
( エ )について、たとえば( ウ )で考えた図において、電子がBの左側ではなく真上にあると想定した場合、先ほど同様に考えるとFの向きは画面下向きになることがわかります。また、電子がBの右側にあればFは左向き、電子がBの真下にあればFは上向きとなり、Fの向きはBを中心として常に内側を指しています。
このように、電子には常にBの位置に近づこうとする力が掛かりますが、一方で、カーブしようとする物体には遠心力が掛かります。この遠心力は、ローレンツ力と全く同じ大きさであり、かつ、反対向きとなっています。
よって、ローレンツ力と遠心力とのバランスにより、電子はBの位置まで吸い寄せられることはなく、常に一定の距離を保ったまま「円運動」することになります。

コメント