電験三種 H28年 理論 問7 問題と解説

　問 題　　　　　

静電容量が1μFのコンデンサ3個を下図のように接続した回路を考える。全てのコンデンサの電圧を500V以下にするために、a-b間に加えることができる最大の電圧V_mの値[V]として、最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし、各コンデンサの初期電荷は零とする。

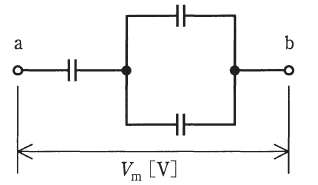
1. 500
2. 625
3. 750
4. 875
5. 1000

 

 

 

 

 

　解 説　　　　

問題文の図に対して、左側のコンデンサの端子電圧をV₁、右側のコンデンサの端子電圧をV₂とすると、下図のようになります(右の2つは並列なので同電圧です)。

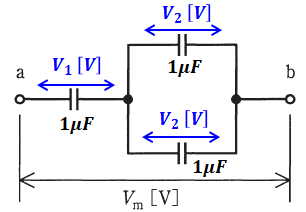
ここで、並列に並んだ2つのコンデンサを合成すると、合成後のコンデンサの静電容量Cは合成前の静電容量の和になります。今回の場合、1+1=2[μF]です。

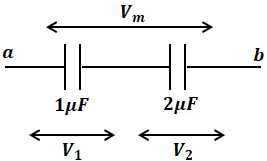
また、直列に並んだ2つのコンデンサに蓄えられる電荷Qは等しいので、Q=CVでQが等しいなら、上図の2つのコンデンサについて、C×Vの値が等しくなります。よって、

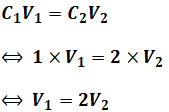
という関係式が導けます。

ここで、V₁とV₂はそれぞれ500V以下とした上でV_mの値を最大にしたいので、V₁とV₂のどちらかは500Vにするべきです。もしV₂を500Vにしてしまうと、上式よりV₁が1000Vになってしまうので不適です。よって、V₁を500Vにするのが正しく、上式より、V₂は250Vとなります。

そうしたら、上図を見てもわかるようにV_mはV₁とV₂の和で表されるので、

と求めることができます。