問 題
図のように、長い線状導体の一部が点Pを中心とする半径r[m]の半円形になっている。この導体に電流I[A]を流すとき、点Pに生じる磁界の大きさH[A/m]はビオ・サバールの法則より求めることができる。Hを表す式として正しいものを、次の(1)~(5)のうちから一つ選べ。

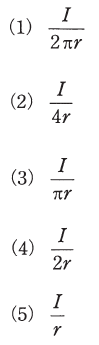
正解 (2)
解 説
ある点において電流が流れるとそこには磁界が生じますが、特に電流が曲線を描く際に、ビオ・サバールの法則という以下の式を使うことで、磁界の大きさを計算によって求めることができます。
![]()
- ΔH:点Pに生じる磁界の大きさ[A/m]
- I:電流[A]
- Δl:微小距離[m]
- θ:Δlとrとのなす角(下図参照)
- r:Δlから点Pまでの距離[m]
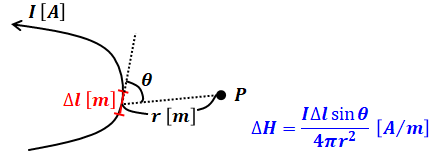
この公式をそのまま覚えておくことが大事ですが、特に、上図の曲線が点Pを中心とした円になっているパターンが多いです。その場合、ビオ・サバールの法則は以下のように書き換えられます。
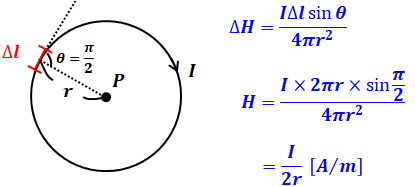
![]()
上図に記載している青字の式において、Δlは円周上の微小距離のことですが、点Pに生じる磁界は外周の全方向を流れる電流の総和によって決まるので、Δlの累積は円周の長さである2πrとなります。
上記の通り円の中心の磁界の式は頻出なので、上式(H=I/2r)はぜひとも押さえておきたい式です。とはいえ、ビオ・サバールの元々の公式からすぐに計算することもできるので、無理に暗記しなくても大丈夫です。
ここで、この問題の話に戻ると、今回は円ではなく半円になっています。よって、上記の円の式(H=I/2r)の半分なので、
![]()
が答えとなります。
または、ビオ・サバールの法則より、
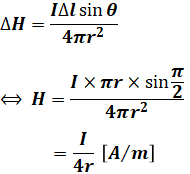
と計算しても構いません。

コメント